TP 06 : Régime Sinusoïdal 1
Ceci est une aide pour l'utilisation d'ISIS Proteus dans le TP6.
1)
Le circuit RC
Pour la simulation prendre V2 = ?? VRMS f = 50 Hz R = 470 Ω C = 10 µF
Simuler le montage et mesurer le courant du
montage.
Avant de lancer la simulation mesurer la tension de sortie du
transformateur
et remplacer V2 par cette valeur.
Calculer la puissance que doit dissiper la résistance R.
Cette puissance est-elle compatible avec une
résistance 1/4 W, 1/2 W, 1 W ou 2 W ?
Si la puissance dépasse 2 W prendre un rhéostat 1000 Ω (320 W
/ 0,57 A)
Mesurer
les valeurs efficaces VR, VC et V2.
La loi des mailles est-elle vérifiée avec les valeurs efficaces ?
Mesurer φC le déphasage
entre VC(t) et VR(t).
VC(t) est-il en avance ou en retard sur i(t) ?
Ces résultats étaient-ils prévisibles ?
Remarque : on utilisera un oscilloscope et cette
méthode pour mesurer le déphasage sur le montage réel.
Voici une vidéo supplémentaire pour expliquer
comment mesurer un déphasage ?
Mesurer φ2 le déphasage entre VR(t) et V2(t). Origine des phases VR(t)
Mesurer φ2/C le déphasage entre VC(t) et V2(t). Origine des phases V2(t)
Ecrire en nombre complexe sous forme polaire
V2,
VR et
VC.
Puis convertir ces nombres sous forme cartésienne.
La loi des mailles est-elle vérifiée en utilisant l’écriture
complexe ?
Aide vidéo Proteus :
Etape 1 : Pick device (RES CAP INDUCTOR)
Etape 2
: Placer des
Instruments Virtuels (Ampèremètre et Voltmètre)
Etape 3 : Placer une sonde différentielle pour mesurer VR. Mesurer un déphasage.
Attention : sortie directe d’un transformateur
Les courants peuvent être très importants !
Court Circuit = dégâts
matériels !
Brancher 2 masses sur un oscillo peut créer un CC
Condensateur chimique sur sortie d’un transformateur = explosion !
Réaliser ce montage et remplir ce tableau récapitulatif :
|
|
V2 en V |
VR en V |
VC en V |
φ2 en ° |
|
Simulation |
|
|
|
|
|
Mesures exp. |
|
|
|
|
|
Comparaison en % |
|
|
|
|
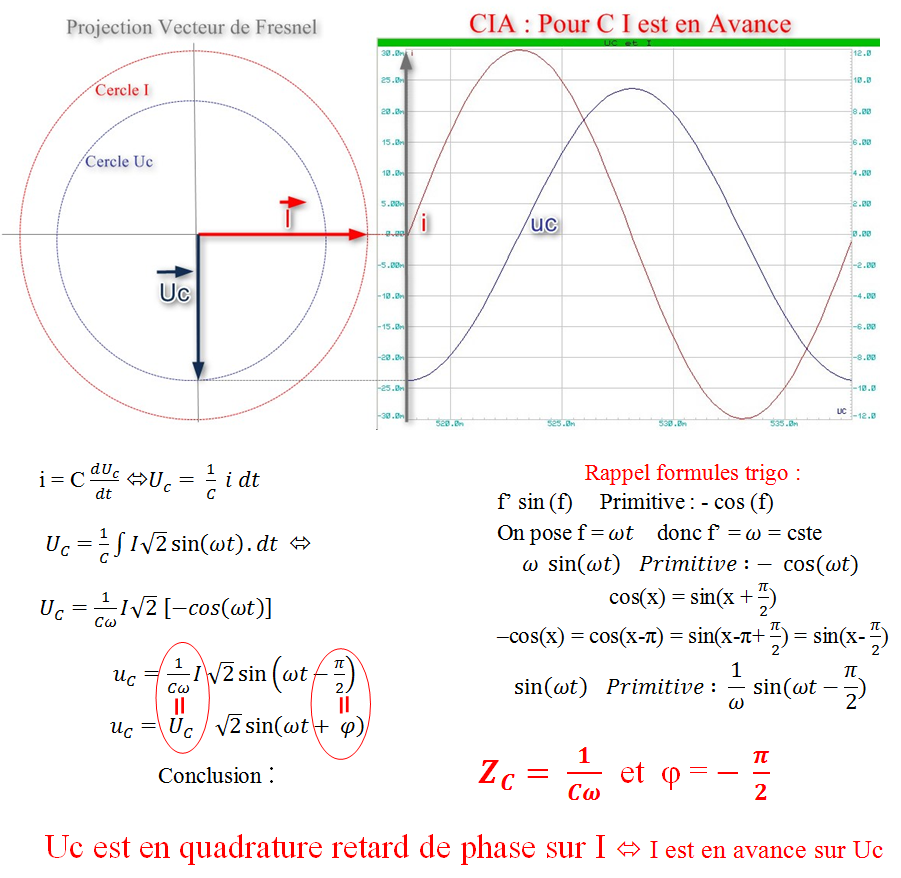
Complément de cours :
Origine des phases :
Pour un circuit série, la grandeur commune à tous les
éléments du circuit est l’intensité I.
On prendra donc comme origine des phases I. Un zéro front montant de
i nous fera travailler en sinus :
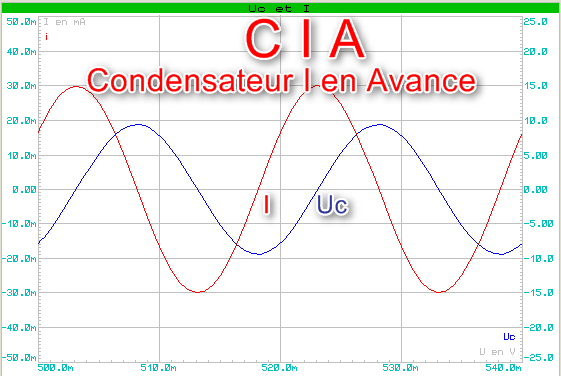
Analyse C I A :
=>
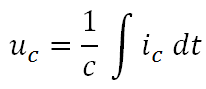
Le Condensateur est chargé par le courant I, ce qui entraîne une
accumulation (intégration) de charges sur les armatures du
condensateur
ce qui fait augmenter sa tension Uc.
Mnémotechnique :
Pour C I est en Avance (C I A) ou pour C I est devant V (C I V).
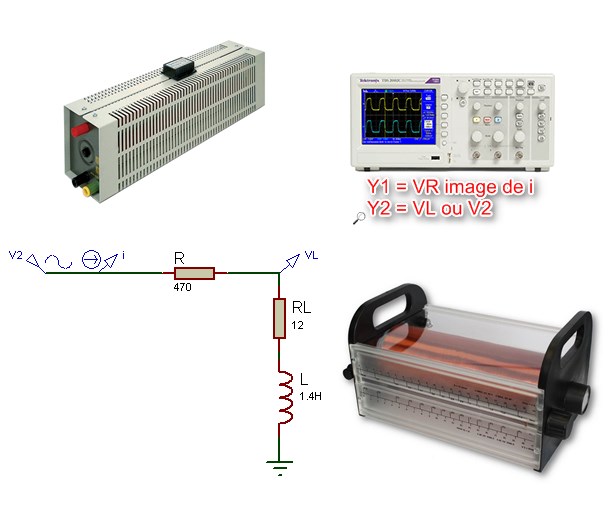2)
Le circuit RL
En électrotechnique (moteur, transformateur,
lissage du courant…) nous utilisons très souvent des bobines (
inductance L en Henry).
Nous ne
disposons pas de bobine parfaite, la résistance RL
modélise la résistance des fils de la bobine.
L = 1,4 H, RL = 12 Ω
R = 470 Ω
Simuler le montage sur ISIS Proteus et mesurer le courant du montage.
Calculer la puissance que doit dissiper la résistance R. Choisir la résistance adéquate.
Mesurer VR, VL et V2.
La loi des mailles est-elle vérifiée avec les valeurs efficaces ?
Mesurer φL le déphasage entre
VL et VR.
VL est-il en avance ou en retard sur i ?
Ces résultats étaient-ils prévisibles ?
Mesurer φ2 le déphasage entre V2 et VR.
Ecrire en nombre complexe sous forme
polaire V2,
VR et
VL.
Puis convertir ces nombres sous forme cartésienne.
La loi des mailles est-elle vérifiée en utilisant l’écriture
complexe ?
Aide vidéo Proteus :
Etape 4
: Placer une sonde de courant et utiliser 2 échelles différentes sur
un graphe
Réaliser ce montage et remplir ce tableau récapitulatif :
|
|
V2 en V |
VR en V |
VL en V |
φ2 en ° |
|
Simulation |
|
|
|
|
|
Mesures exp. |
|
|
|
|
|
Comparaison en % |
|
|
|
|
Mnémotechnique : C I V I L
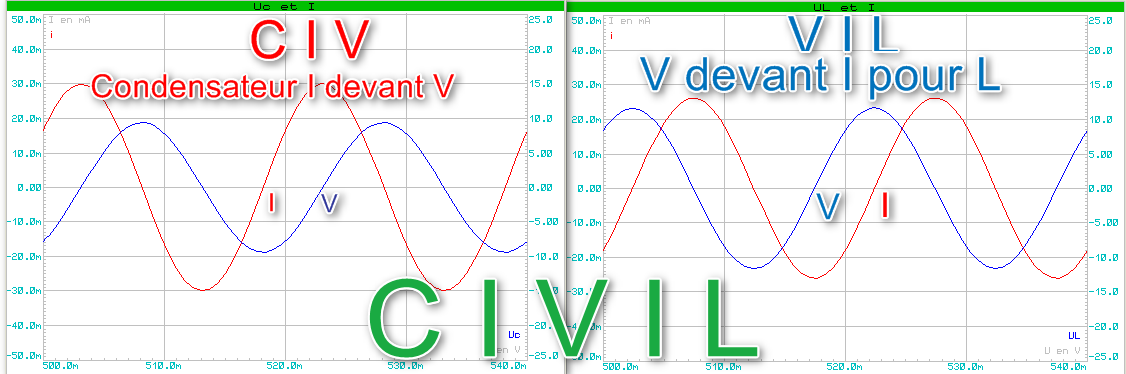
Analyse : V I L
La force électromagnétique V
entraîne la mise en mouvement des électrons et donc l’apparition
d’un courant I pour
L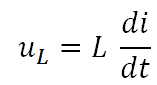 
Analogie électro-mécanique
Les équations différentielles des circuits électriques R, L, C et des systèmes mécaniques masse (m) , ressort (k) avec frottements visqueux (λ) sont semblables.
L’analyse de ces équations nous montre qu’une analogie électro-mécanique est possible :
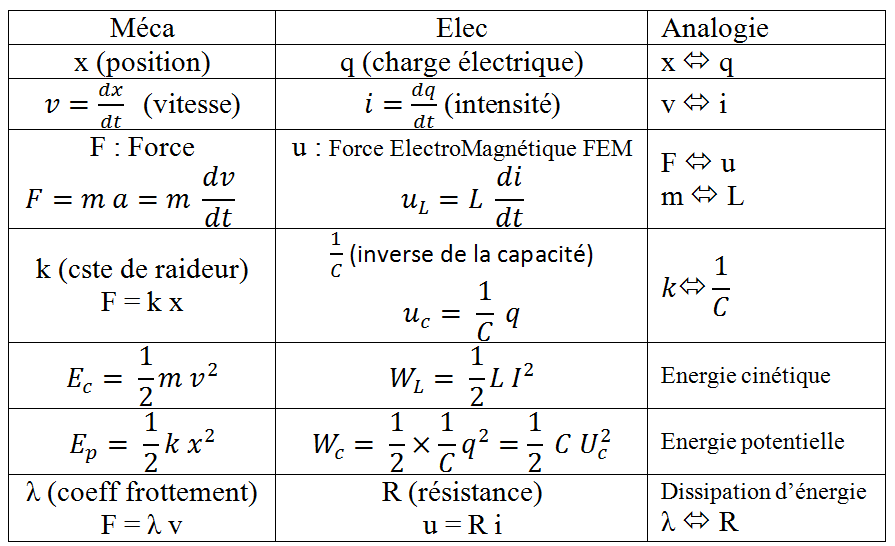
La démo du jour :
