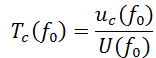TP 07 : Régime Sinusoïdal 2 / Résonance d'un circuit R L C
Ceci est une aide pour l'utilisation d'ISIS Proteus dans le TP9.
Le circuit R L C
Simulation sur Proteus. Réaliser ce montage à l’aide de Proteus.
Régler la position du noyau de fer pour avoir L = 1H,
prendre R = 47, ne pas oublier RL = 12 Ω.
La résistance interne du GBF de 50 Ω n'est pas prise en compte car
lors de la partie expérimentale
cela sera à vous de la compenser en maintenant la tension du GBF à
1VRMS
Les résultats seont à reporter dans ce
tableau Excel.
Les courbes seront ainsi tracées automatiquement.
Tracer en concordance de phase Ur et U pour f = 100 Hz puis f = 200
Hz
Mesurer le déphasage pour chacune de ces fréquences.
A 100 Hz le circuit est plutôt inductif ou capacitif ?
A 200 Hz le circuit est plutôt inductif ou capacitif ?
Aide vidéo Proteus :
Etape 1 : Mesurer un déphasage et utiliser 2 échelles Y
différentes.
Tracer la fonction de transfert
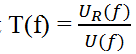
Imprimez cette caractéristique et annotez-la.
Etape 2 : Tracer une caractéristique fonction de la fréquence T(f). Courbes : FREQUENCY REPONSE
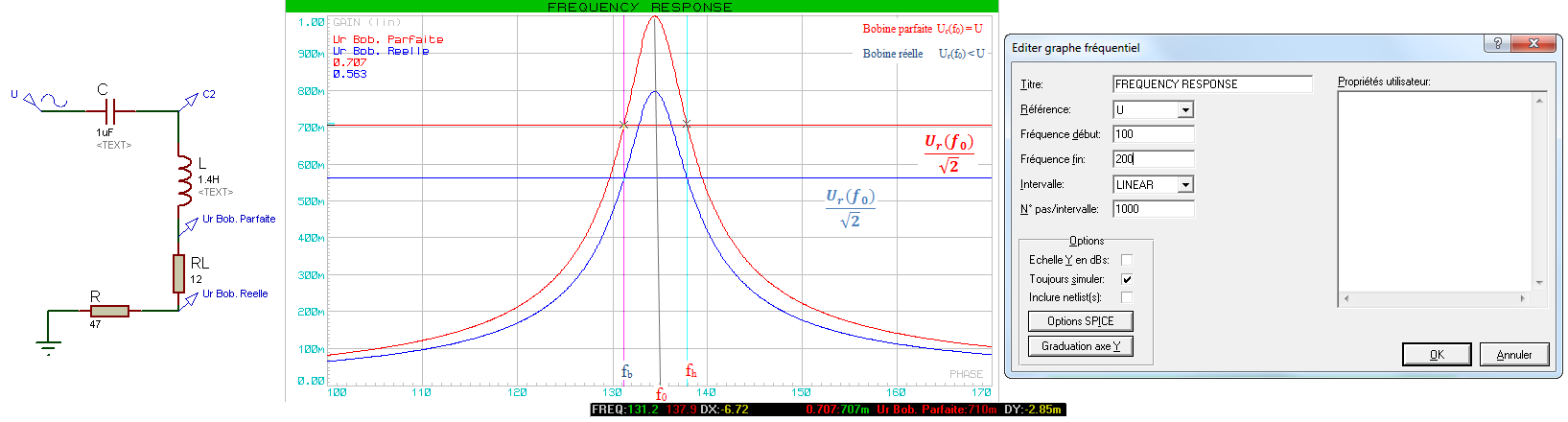
Annotations à apporter :
-
Traits de construction pour la bande passante (f0, fb et fh)
-
Report des valeurs des curseurs pour f0, fb , fh et Δf = DX
-
Calcul du facteur de qualité
-
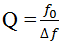
Nom de chaque courbe, titre du graphique ...
Différence entre bobine parfaite et bobine réelle :
-
à f = f0 pour la bobine réelle Ur < U alors que Ur = U pour la bobine réelle soit T = 1
-
bande passante identique si on prend pour la bobine parfaite R' = R + RL
Déterminer la fréquence de résonance f0
A f0 que vaut le déphasage ?
Déterminer la bande passante Δf (intervalle de fréquence Δf
pour lequel
)
Joindre la courbe et la construction permettant de déterminer cette bande passante.
En déduire le facteur de qualité
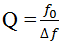de ce filtre passe bande.
Tracer le diagramme de phase.
Que vaut la phase aux fréquences de coupure (lorsque
)(Annoter la courbe obtenue)
Que devient la bande passante Δf’ et le facteur de qualité Q’ lorsque R’= 470 + 12 = 482 Ω ? (Annoter la courbe obtenue)
Tracer sur le même graphe les fonctions de transfert (mode bobine
parfaite) correspondant à
R = 47 +12 = 59 Ω, R’’= 259 + 12 = 271 Ω et R’ =
470 + 12 = 482 Ω pour f variant de 100 à 250 Hz.
Annoter sur le graphe la valeur de résistance correspondant à chaque
courbe.
Annoter le graphe pour y faire apparaître les 3 bandes passantes
correspondantes.
Etape 3 : Tracer des courbes paramétrées par R. Courbes : AC SWEEP ANALYSIS
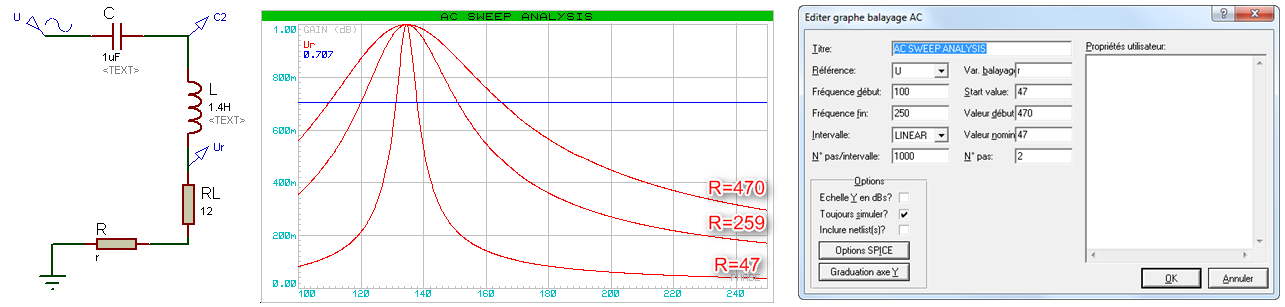
On souhaite maintenant visualiser pour les 3 résistances R, R’ et
R’’ l’allure de la fonction de transfert
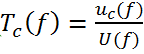
Etape
4
: Courbes paramétrées par R
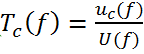Courbes : AC SWEEP ANALYSIS
Comparer la tension maximale de Uc à celle mesurée
Comparer les valeurs obtenus au facteur de qualité Q obtenu
pour chaque filtre.
Annoter sur le graphe la valeur de résistance correspondant à chaque
courbe.
Annoter le graphe pour y faire apparaître les valeurs maximales de
chaque courbe
Tableau récapitulatif :
|
R en Ω |
F0 en Hz |
Fb en Hz |
Fh en Hz |
|
|
|
R = 47+12 Ω
|
|
|
|
|
|
|
R’ = 259+12 Ω
|
|
|
|
|
|
|
R‘’= 470+12 Ω
|
|
|
|
|
|
Reprendre l'ensemble de l'étude de manière expérimentale.
Reporter vos mesures dans ce tableau Excel et tracer les courbes demandées.