Monte-Carlo
1) Estimer Pi en jouant aux dés
Le terme méthode de Monte-Carlo, ou méthode Monte-Carlo, désigne
une famille de méthodes algorithmiques visant à calculer une valeur
numérique approchée en utilisant des procédés aléatoires,
c'est-à-dire des techniques probabilistes.
Wikipédia
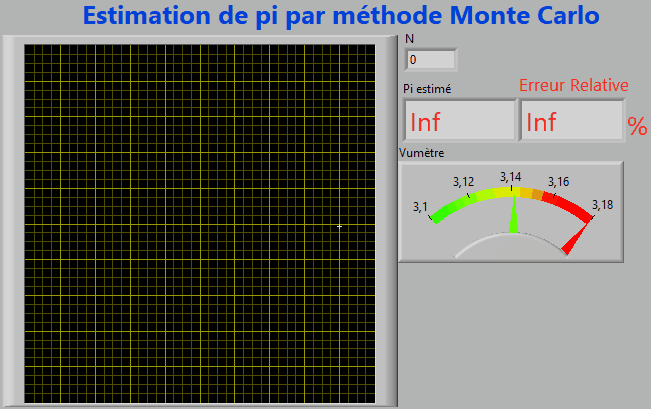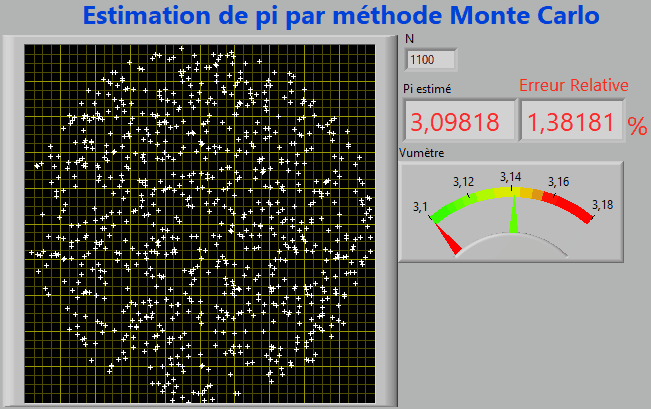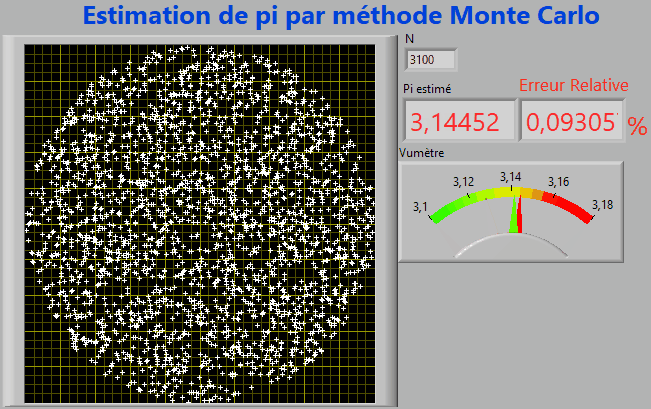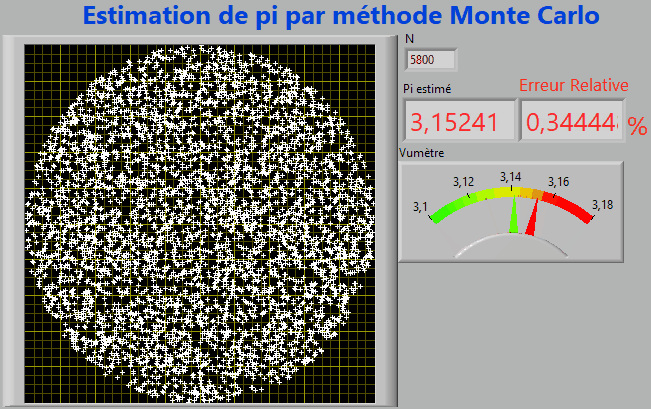
- Le calcul de π par la méthode de Monte-Carlo consiste à tirer au hasard des nombres x et y dans l'intervalle [-1 ; 1].
- Tous les points M (x, y) sont contenus dans un carré de surface S = 2*2 = 4
- Si x2 + y2 ≤ 1 le point M (x, y) appartient au disque de rayon R=1 et de surface π.R2 =π
- N est le nombre total de points générés par une suite
pseudo-aléatoire,
p est le nombre de points à l'intérieur du disque.
Le rapport p/N est égal au rapport des surfaces π/4
1. Estimer π en fonction de S, N et p.
On peut constater ici qu'une méthode Monte-Carlo permet d'estimer une surface, donc une intégrale.
En métrologie, le calcul d'un risque revient à calculer des intégrales très complexes.
La méthode Monte-Carlo et la simulation numérique permettent d'estimer plus simplement les risques.
Pour être efficace une simulation type Monte-Carlo doit reposer sur un échantillon N de grande taille.
Télécharger le VI en cliquant sur l'image de l'algorithme ci-dessus.
Pour être performant nous allons prendre un échantillon N important N=100000
Pour estimer notre incertitude nous allons répéter un grand nombre de fois cette simulation.
2. Pour estimer π nous avons utilisé 2 variables
aléatoires x et y
qui suivent une loi uniforme (comme un dé
)
L'estimation de π obtenue suit-elle
une loi uniforme elle-aussi ? (joindre une capture d'écran)
A l'aide du
théorème central limite jutifiez l'omniprésence de la
loi normale dans la nature.
Planche de Galton : la loi binomiale converge vers la loi normale .Wikipédia
3. La loi de Student dans l'échantillonnage est
valable pour des variables indépendantes suivant quelle loi ?
Est-ce le cas ici ?
Repérer dans le programme la partie qui
calcule l'intervalle de confiance à 95% selon la loi de Student.
Joindre une capture d'écran annotée dans le compte rendu
4. L'intervalle de confiance diminue au fur à
mesure que la simulation se déroule.
Cette diminution est-elle linéaire ?
Justifiez votre réponse.
5. Dans cette simulation nous disposons de la
valeur vraie et la valeur estimée.
L'intervalle de confiance établi grâce à la loi de Student vous
semble-t-il fiable ?
Joindre une capture d'écran annotée dans le compte rendu pour
justifier votre réponse.
6. Jusitfiez : "Pour être efficace une simulation type Monte-Carlo doit reposer sur un échantillon N de grande taille."
Nous allons maintenant utiliser la méthode Monte-Carlo pour estimer la propagation des incertitudes dans une chaîne de mesure.
2) Simulation de notre modèle PT100
Comme
dans le TP précédent nous allons construire un VI simulant une
mesure correspondant à un mesurande donné.
Aujourd'hui nous allons simuler la réponse de la PT100 associée au transmetteur disponible au labo J101.
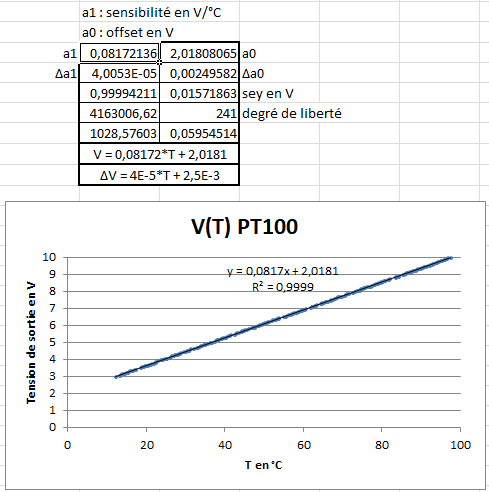
Pour calculer V(T) nous utiliserons les résultats obtenus lors du TP étalonnage d'une PT100
Vous pouvez aussi utiliser les données disponibles sur ce lien ou la figure de synthèse de la fonction droitereg ci-contre.
7. Quelle équation faut-il utiliser pour calculer la tension correspondant à une température T ?
8. Quelle équation nous permet de calculer l'incertitude-type de notre modèle ?
9. A l'aide de ces équations et d'une méthode Monte-Carlo associez une mesure en Volt à un mesurande T.
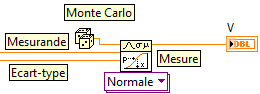
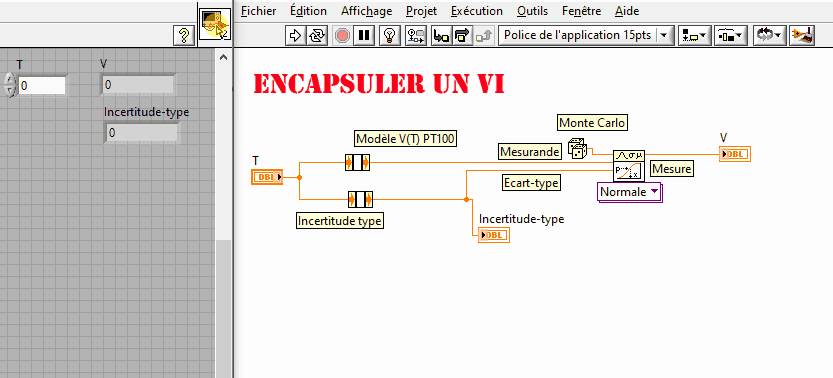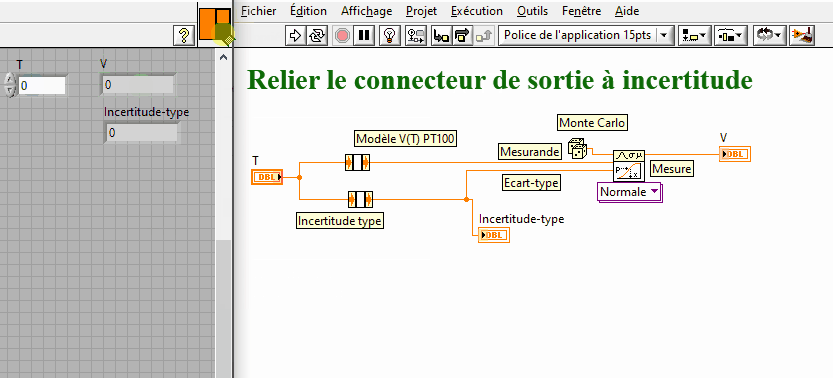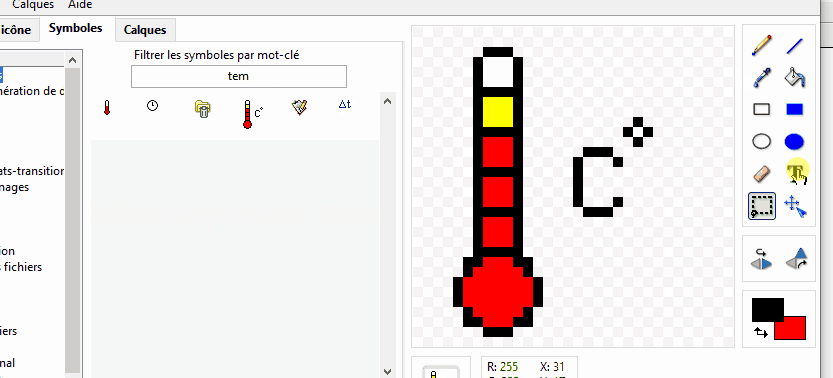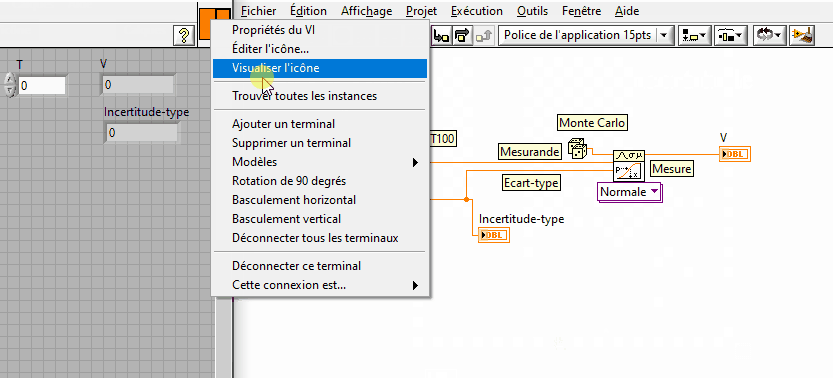
Encapsulez le VI 
pourqu'il réponde au cahier des charges ci-dessous :
Besoin d'aide ? Labview for dummies
3) Propagation des incertitudes dans une chaîne de mesure
Nous avons identifié 3 sources d'incertitude dans notre chaîne de
mesure.
- La sonde de température utilisée comme étalon.
La doc constructeur(ci-contre) nous annonce une précision de 0,3°C.
U=0,3°C Uncertainty = Incertitude élargie = k*Incertitude-type = k*u
Sans plus de précision, nous supposons que l'intervalle de confiance pris par le constructeur est de 95%
soit un facteur d'élargissement : k = 2.
Nous en déduisons que son incertitude-type est s = u = U/k = 0,3/2 = 0,15°C
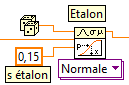
- La modélisation de notre PT100 associée à son transmetteur.
Pour cela nous utiliserons le sous-vi encapsulé à la partie 2
- Le multimètre FI2960MT est lui aussi source d'incertitude
Si vous avez perdu ce sous-vi programmé la semaine dernière,
cliquez sur l'image pour le télécharger.
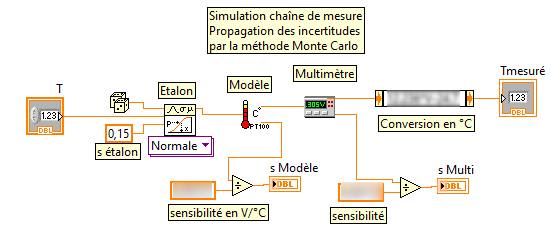
10. Programmez la chaîne de mesure.
Pour un mesurande T afficher la température mesurée
et les incertitudes de chaque élément de la chaîne.
La méthode de Monte Carlo est valable à condition d'effectuer un
grand nombre de simulation.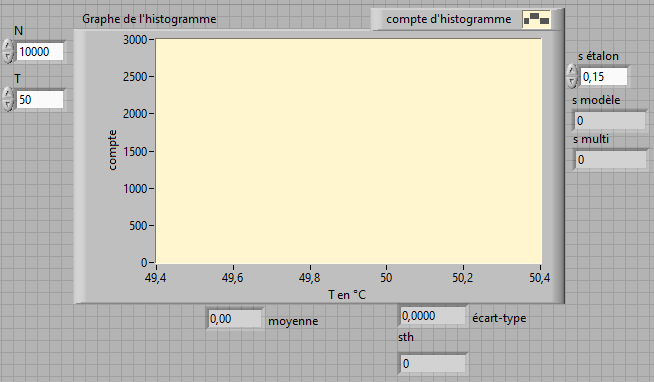
11. A l'aide d'une boucle for, répéter N fois la
mesure.
Faire un traitement statistique et afficher :
- l'histogramme des fréquences
- la valeur moyenne
- l'écart-type
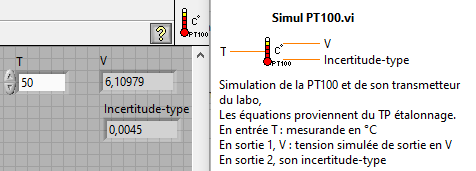
12. La face avant souhaitée est ci-contre
13. Faire une capture d'écran pour N=10000 et T=50°C
14. Comparer l'écart type de la chaîne de mesure aux écarts-types de chaque élément.
15. Est-ce que l'écart type de la température mesurée est la somme des écarts-types ?
16.
Si cela n'est pas le cas proposez une relation entre les
écarts-types.
Programmez cette relation dans une boîte de calcul.
Vérifiez si cette relation est conforme à vos simulations.
17. Faire une capture d'écran pour N=10000 et T=5°C
18.
Faire une capture d'écran pour N=10000 et T=100°C
Que remarquez-vous sur s multi ? Pourquoi ?
19. La simulation Monte-Carlo a-t-elle permis de confirmer la loi de propagation des incertitudes que nous connaissons ?