Courbes

Prévision trajectoire du BBR8

Ce site nous a permis de simuler la trajectoire du ballon sonde à compter de 6 jours avant le lâcher.

La simulation réalisée la veille, qui s'est révélée fiable, nous a conforté dans la décision de lâcher le ballon le 13 mai malgré les pluies éparses prévues ce jour-là.

Par contre, la pluie a mouillé le ballon au départ. Arrivé en altitude celle-ci a dû geler, ce qui a fait éclater notre ballon prématurément à 21 000 m contre les 30 000 m prévu.

Merci à l'association Planète Sciences d'avoir rendu possible cette aventure Scientifique et Technique hors du Laboratoire à nos terminales STL et à nos BTS TPIL.

Merci à notre suiveur et aérotechnicien Jean Claude Desarnaud pour ses conseils, son soutien technique et sa disponibilité.

Suivi Trajectoire

Les mesures brutes au format Excel

Lien direct Fusion tables

Lien direct Map

Eclatement

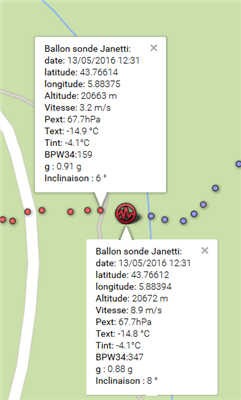
On note au moment de l'éclatement à 12h31 et 17 s (à 2s près) après un vol de 1h24 et 18 s soit 5 058 s :

l'altitude est à son maximum : 20 672 m ( 5 058 s * 4 m/s = 20 232 m + altitude de départ 310 m)
la norme de la vitesse augmente brutalement de 3,2 m/s à 8,9 m/s (tout en prenant une direction opposée)
la luminosité mesurée par la photodiode BPW34 orientée vers le haut fait un bond : de 159 à 347
le ballon ne fait plus d'ombre...
la norme de l'accélération diminue à 0,88 g : nous sommes en partie en chute libre dans le référentiel du ballon

Calcul du rayon du ballon au moment de l’éclatement d’après les données collectées

Etat 1 : décollage P₁= 1000 hPa V₁ = 5,9 m³ et T₁ = 17+273 = 290 K

Calcul du rayon du ballon :

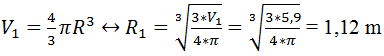
Ce qui correspond bien au diamètre de 2 m qu'avait notre ballon au moment du lâcher.

Nous en déduisons donc le nombre de moles He captives dans notre ballon à l’aide de la loi des gaz parfaits :

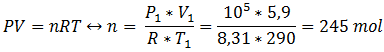
Ce qui représente une masse de : m = n M = 245*4 = 979 g

Les 2 « grosses bouteilles de 40 kg » utilisées n’ont injecté que 979 g d’Hélium dans les 5,9 m³ du ballon !

Pour Maxime : accrocher le ballon à une bouteille "vide" de 40,0 kg l'empêche autant de s'envoler qu'une bouteille "pleine" de 40,5 kg !

Etat 2 : éclatement P₂= 67,7 hPa V₂ = ? et T₂ = -15+273 = 258 K

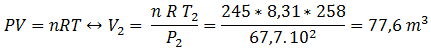
Au moment de l’éclatement notre ballon avait donc un rayon de :

Soit 5,3 m de diamètre (dans les conditions optimales, l’enveloppe du ballon peut supporter jusqu’à 10 m de diamètre)

Remarque : la mesure d'une faible pression avec le type de capteur utilisé n'est pas très fiable.
D'après le modèle de l'atmosphère normalisée nous aurions dû avoir 52 hPa.
Avec cette valeur, on trouve un rayon de 2,9 m soit un diamètre de 5,8 m.

Vitesse ascensionnelle

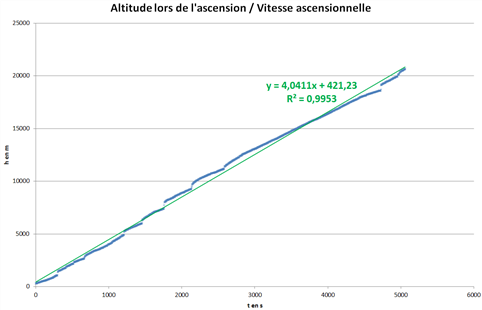Nous constatons bien que lors de l'ascension, la vitesse ascensionnelle est quasi constante et vaut : 4 m/s

comme nous le montre la modélisation de l'ascension h(t) par une droite ci-contre. La vitesse est le coefficient directeur de cette droite.

Remarque : la vitesse mesurée par le GPS est la vitesse résultante des 3 composantes V_x, V_y et V_z (vitesse ascensionnelle).

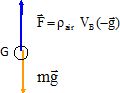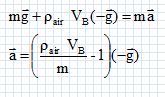Le ballon est soumis à son poids et à la poussée d'Archimède. La vitesse étant quasi-nulle juste après le décollage, la force de frottement est négligeable.

Pour le détail des calculs : Ballon sonde : concours technicien météo 2011.

Cette étude théorique montre qu'un ballon météo de 9 m³ atteint en 1 s sa vitesse limite qui est de 5 m/s pour une nacelle+équipement de 2,5 kg.
Un calcul analogue, effectué par Jean Claude Desarnaud, (en ne négligeant pas les forces de frottement) et avec les valeurs de notre ballon (5,9 m³ ...) et sa chaîne de vol montre que l'on atteint la vitesse limite de 4 m/s en 4 s.

Cela correspond bien à notre expérience.

Remarque sur la poussée d'Archimède : avec l'altidude V_B augmente alors que la masse volumique de l'air diminue...

Pression en hPa en fonction du temps

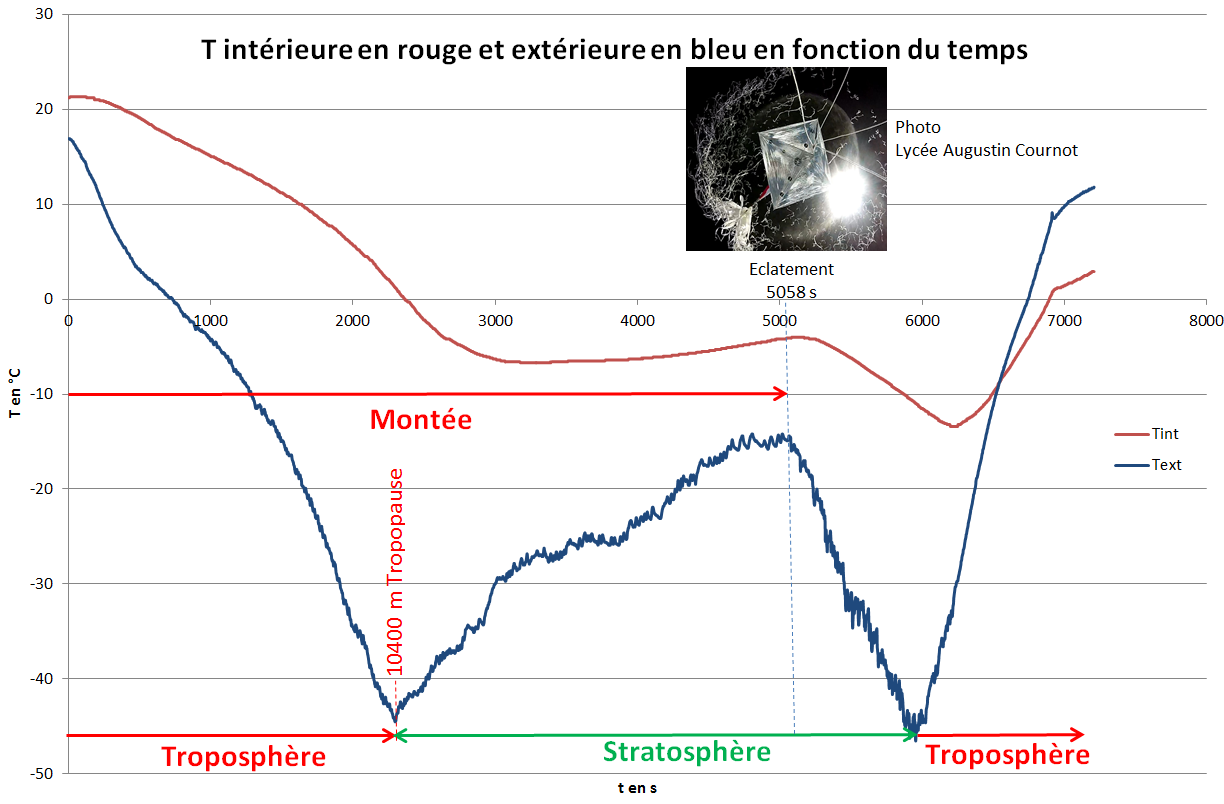
Text en °C en fonction du temps

Analyse température

Là aussi les résultats sont conformes à notre attente :

le minimum de température -44,5 °C est atteint à 10 400 m soit le haut de la troposphère
on constate une inversion de l'évolution de la température à cet endroit : la tropopause
puis la température remonte dans la stratosphère grâce à l'absorption des UV par la couche d'ozone (cliquez sur le schéma...)
Dans la troposphère, la température diminue avec l'altitude, à peu près de 6,4 °C tous les 1 000 mètres.
Pour une montée dh = 10 000 m correspond une baisse dt = 10* 6,4 = 64 °C.
Au sol t = 17°C => en théorie 17-64 = -47°C on mesure -44,5°C : c’est cohérent…

Le polystyrène extrudé de la nacelle a bien joué son rôle d'isolant.
Nous sommes quasiment jamais descendu en dessous de -10 °C alors qu'à l'extérieur la température est descendue à -45°C.

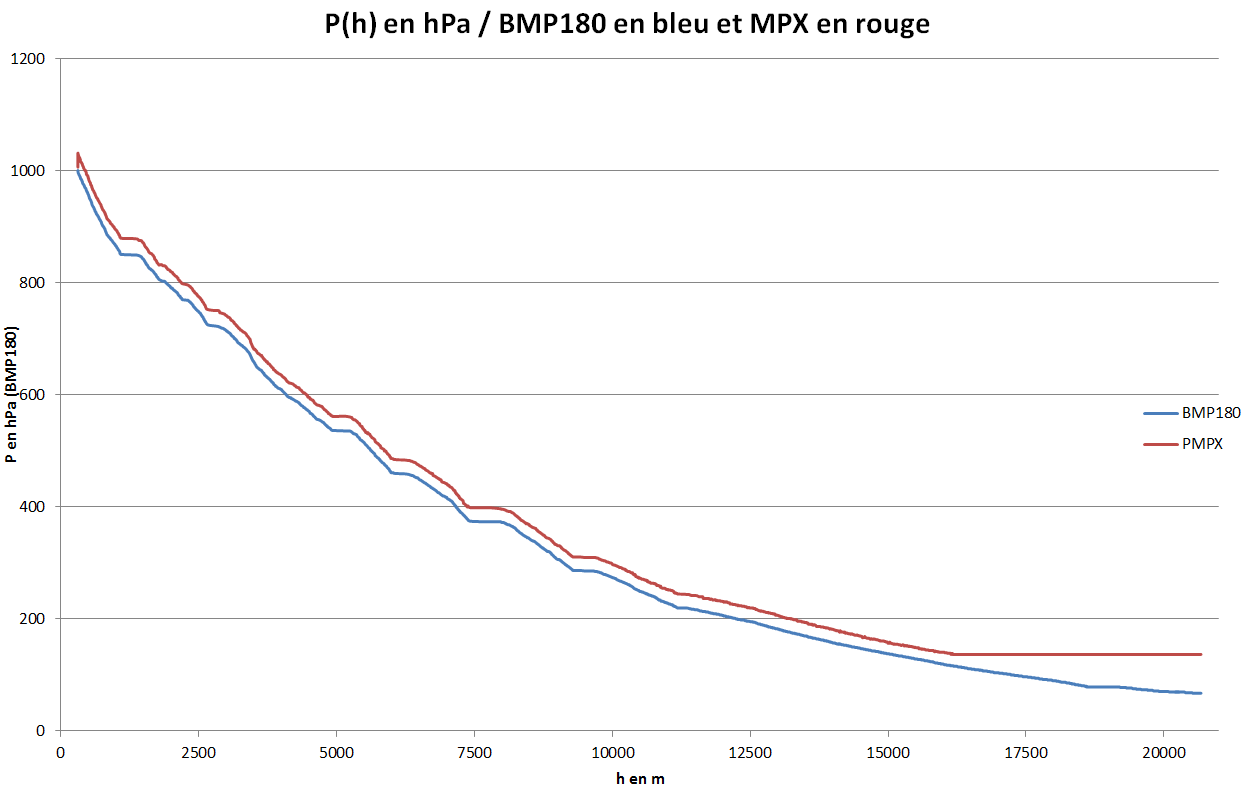
P en hPa en fonction de l'altitude h en m : P(h)

La courbe de pression est elle aussi proche de l'étude théorique menée dans cet exercice de physique : Etude de la pression en fonction de l'altitude, équilibre polytropique de l'atmosphère, ascension d'un ballon

Cette étude donne pour équation : P = P₀ e(-0,00012*h)
(pour une atmosphère en équilibre isotherme à 15 °C : c'est le point faible de ce modèle car T varie...)

Cependant la modélisation de notre courbe nous donne un résultat assez proche :

Pour être plus réalistes, nous avons comparé nos mesures à l'atmosphère OACI qui sert à l'étalonnage de tous les altimètres des avions volant dans le monde.

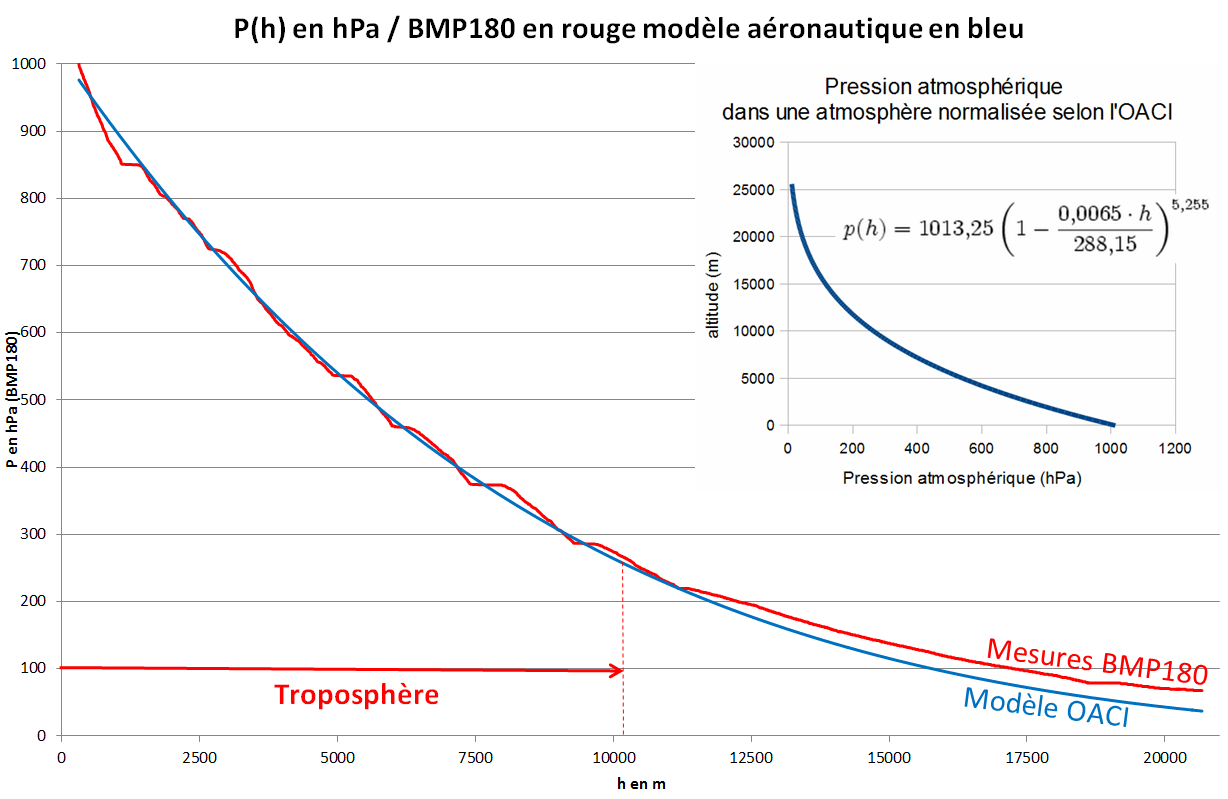
Nos mesures sont cohérentes avec le modèle, par contre on note un décrochement d'environ 20 hPa au delà des 12 000 m.
Ce décalage quasi-constant provient peut-être d'une erreur d'étalonnage pour les faibles pressions.
L’étalonnage a été réalisé avec un Jeulin Initio (±4 hPa) qui n'est pas adapté aux basses pressions... D'autant plus qu'aucun Jeulin du labo n'indique la même pression...
De plus nous sommes largement hors de la gamme de mesure préconisée par le constructeur du BMP 180 (300 à 1100 hPa).
L'exactitude et la fidélité du capteur ne sont plus garanties...
Cette divergence intervient après la troposphère lorsque la courbe de température s'inverse.
L'équation de l'OACI utilisée pour tracer le modèle n'est valable que dans la troposphère.

Par curiosité nous avons comparé nos deux capteurs de pression analogique MPX5100 et numérique BMP180.
Nous avions remarqué que l'émetteur Kiwi perturbait le MPX qui surévaluait alors la pression. Au final ce défaut se comporte comme un décalage constant.
On constate aussi que le MPX ne descend pas en dessous de 137 hPa ce qui correspond à une altitude de 16000 m environ.

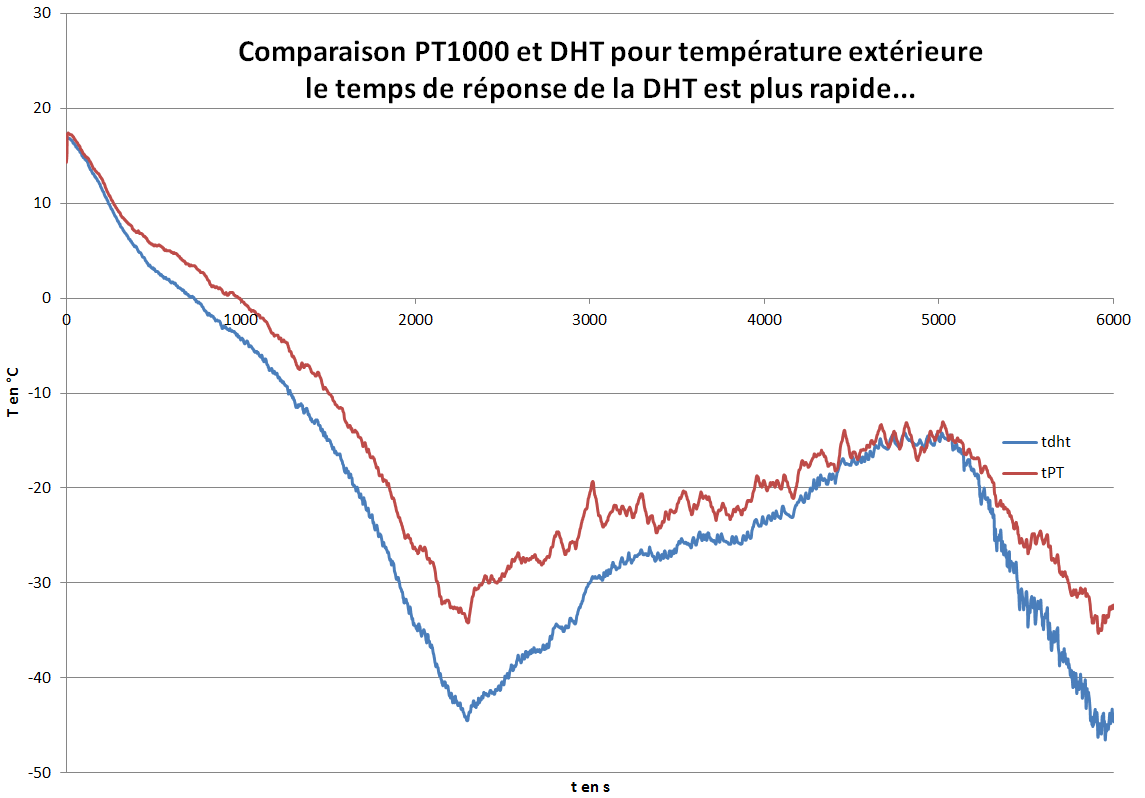
Comparaison PT1000 et DHT22

La PT1000 est un capteur analogique associé à un montage à 2 ampliOp. Il est sensible aux perturbations électromagnétiques de l'émetteur Kiwi : on a du l'éloigner le plus possible de l'émetteur.
De plus son temps de réponse n'est pas assez rapide pour suivre fidèlement les variations de température à l'extérieur du ballon comme nous le montre les courbes comparatives ci-dessous.
Les deux capteurs Pt1000 et DHT22 sont situés côte à côte à l'extérieur du ballon.

Le capteur de luminosité - Photodiode BPW34

Comme le montre la vidéo la nacelle n'arrête pas de tourner sur elle même. C'est pour cela que la luminosité varie sans cesse selon que le capteur soit orienté au sud ou au nord.

Il faut donc travailler avec l'enveloppe supérieure de la courbe.

On constate la variation importante de luminosité :

au moment du lâcher 57 soit 0,223 V ce qui correspond d'après notre étalonnage à _____ lux
au maximum on atteint 401 soit 1,96 V ce qui correspond d'après notre étalonnage à _____ lux