Capteur de force - Pont de Wheatstone et HX711

Objectif du TP Capteur de force, Pont de Wheatstone et HX711

Réaliser l’étude complète d’une balance numérique à capteur de force :

Etape 1 : Calculer sa sensibilité théorique à l'aide de l'annexe 1 Fiche de calcul à compléter
Etape 2 : Mise en oeuvre du HX711
Etape 3 : Réaliser l’étalonnage expérimental,
Etape 4 : Évaluer la fidélité et l’incertitude globale du système,
Apprendre à rédiger une conclusion sur la justesse, la fidélité et l'exactitude
Finaliser l'annexe 2 : PV étalonnage disponible sur ce lien
Etape 5 : Réaliser une Balance 100% Arduino (sans PC)

Compte rendu à rendre

Consigne :

Téléchargez le document réponse et complétez-le tout au long du TP.

Le compte rendu doit être remis à la fin du TP.

Résultats à reporter :

Les résultats des parties 3 et 4 doivent être saisis dans le fichier Excel TP_09_Balance_Excel

Les tableaux correspondants sont déjà préparés.

Annexes à joindre au compte rendu :

Annexe 1 – Fiche de calcul (complétée)
Annexe 2 : PV d’étalonnage (TP_09_Balance_Excel ) prérempli à compléter avec résultats, graphiques et conclusion.

Contexte professionnel

La maîtrise des masses et des quantités de matière est un enjeu de sûreté majeur dans l'industrie,
notamment dans le secteur nucléaire (gestion des combustibles, contrôle des effluents) ou la chimie fine.
L'exigence de traçabilité et de fiabilité des mesures impose une qualification métrologique totale, quelle que soit la complexité de l'instrument.

Ce Travail Pratique se concentre sur l'analyse approfondie d'un système de pesage (une balance) de démonstration.
Il est crucial de noter que le corps d'épreuve avec jauge de contrainte utilisé dans cette balance
est exactement le même que celui que l'on trouve dans les balances de laboratoire
ou les systèmes de pesage industriels de haute précision.

L'objectif n'est donc pas l'outil lui-même,
mais la démonstration qu'une caractérisation rigoureuse peut transformer n'importe quel montage,
dès lors qu'il utilise des capteurs de qualité, en un instrument fiable et conforme.

Notre démarche professionnelle se concentrera sur l'atteinte de la meilleure exactitude de mesure par :

L'Étalonnage : Correction des erreurs systématiques (justesse).
La Réduction de l'Incertitude : Quantification du défaut de fidélité par le budget d'incertitude.

L'aboutissement est la preuve que la méthodologie métrologique permet d'obtenir,
pour une portée de1kg, une fidélité et une justesse comparable à celles des équipements professionnels.

Ce TP souligne que la compétence de l'ingénieur métrologue est la clé de la qualité de la mesure.

Jauge de contrainte

La jauge d'extensométrie permet de mesurer de faibles déformations.

Il s’agit d'un fil conducteur très fin (épaisseur 2 microns) de longueur L et de section S collé sur un support plastique.

Sa résistance au repos vaut

Le volume du fil conducteur L*S est constant.

R+ΔR : en traction la jauge s’allonge, L augmente et S diminue → ρ.L/S augmente de ΔR
R-ΔR : en compression la jauge se rétracte, L diminue et S augmente → ρ.L/S diminue de ΔR

On associe cette jauge d'extensométrie à un corps d’épreuve métallique usiné de façon à se déformer sous la pression (contrainte) d’une force que l’on souhaite mesurer.

Le corps d’épreuve est conçu pour présenter 2 zones de compression et 2 zones de traction. Il peut ainsi recevoir 4 jauges.

L’association jauge + corps d’épreuve = jauge de contrainte et constitue un capteur de force.

En changeant la forme du corps d'épreuve on peut aussi réaliser un capteur de couple.

Exemple d’un capteur de force de 1 kg :

D'après la doc technique : R = 1000 Ω

Pour la charge pleine échelle (1kg ici) : R-ΔR ≈ 998 Ω, soit ΔR ≈ 2 Ω et ΔR/R ≈ 0,002

ΔR/R est proportionnel à la contrainte subie par le corps d’épreuve et donc à la force.

La documentation technique nous donne la sensibilité nominale en mV/V au lieu de ΔR/R.

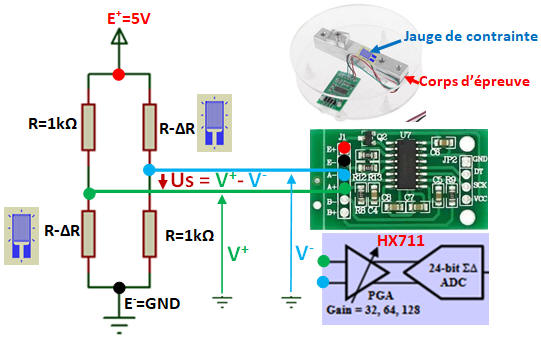Pont de Wheatstone

Le pont de Wheatstone permet de convertir ΔR/R en une tension électrique cf la fiche de calcul.

Le pont complet à 4 jauges est le plus performant en sensibilité, linéarité…
Il est aussi le moins sensible à la dérive en température.

On peut se contenter d’un demi-pont à 2 jauges que l’on complète avec deux résistances R.
Notre capteur de force incorpore les résistances R au plus près des jauges afin de limiter l’importance de la résistance des fils.

Il existe aussi un quart de pont qui ne comporte qu’une jauge complété par 3 résistances R.

Avec notre capteur en sortie de pont, pour une charge pleine échelle, nous obtenons une tension de 5 mV.

C’est le Hx711 qui nous permettra d’exploiter cette faible tension et d’obtenir une sortie numérique.

Le Hx711 amplifie d'un facteur 128 ce signal puis le numérise grace à un CAN ΔƩ 24bits à faible bruit.
La structure ΔƩ à 80% numérique du CAN incorpore des filtres numériques.
Un peu lent (10 échantillonnages par seconde) mais parfaitement adapté à notre application.

Étape 1 : Calculs préliminaires

Avant toute manipulation, remplir intégralement l’annexe 1.
Ces calculs permettront de déterminer la sensibilité théorique du montage (Pont + HX711).

Téléchargez Annexe 1 et remplissez cette fiche de calcul de la sensibilité du capteur de force étudié.
À l’aide du diviseur de tension, exprimer $V^{+}$ et $V^{-}$ en fonction de $R$ , $Δ R$ et $V_{CC}$ .
En déduire l’expression de la tension de sortie du pont $U_{s} = V^{+} - V^{-}$ .
Pour $V_{CC} = 5 V$ et une sensibilité nominale de 1,0 ± 0,15 mV/V :
- Calculer la tension de sortie à pleine échelle,
- Déterminer la tolérance de sensibilité en %.
Calculer la sensibilité du pont en µV/g.
Après amplification (gain = 128), déterminer la sensibilité amplifiée du montage.
Calculer le quantum du CAN 24 bits pour $V_{ref} = 5 V$ .
En déduire le nombre de LSB correspondant à 1 g puis la sensibilité S₃ = ΔN/Δm (LSB/g).
Comparer cette valeur à celle issue de la future courbe d’étalonnage : la différence est-elle compatible avec la tolérance calculée ?
-> Reporter ces résultats dans la section théorique du PV Excel.

Appel 1 : Présenter votre étude préliminaire au professeur.

Étape 2 : Mise en œuvre expérimentale – Étude du pont de Wheatstone

La bibliothèque HX711 :

Vérifier si la bibliothèque HX711 by Rob Tilllaart est bien installée.

Voir une présentation plus détaillée sur ce lien.

Les méthodes de cette bibliothèque :

.read_average(n) : lecture et moyennage de n valeurs « brutes » .
.tare() : remise à zéro de la valeur de tare.
.get_value(n) : lecture et moyennage de n valeurs « brutes », moins la valeur de tare.
.set_scale(s) : définition de la valeur d’échelle (s = sensibilité du capteur en LSB/g)
.get_units(n) : lecture et moyennage de n valeurs « brutes », moins la valeur de tare, puis mise à l’échelle de la sensibilité

Cahier des charges programme Arduino :

Ecrire un programme Arduino pour communiquer avec le programme Labview déjà écrit.
Le protocole de communication par liaison série à 115200 est le suivant :
Labview : "G" (pour Go) et attend une réponse qui se termine par \n ( LF : inclus dans .println)
Arduino : "112670\n" Il s'agit d'un exemple correspondant à la tension numérisée du pont par le Hx711

Inclure la bibliothèque HX711
Créer un objet HX711 Balance
Etablir une liaison série à 115200 pour communiquer avec Labview
Cabler le Hx711 : DT (dataPin) -> digital 2 Arduino
SCK (clockPin) -> digital 3 Arduino
Utiliser la méthode HX711 .read_average(10)
pour envoyer la moyenne des 10 dernières mesures
temps estimé = 1 s, le HX711 réalise 10 mesures par seconde...

#include "HX711.h"

HX711 Balance; // création de l'objet Balance

int dataPin = 2;   // Selon cablage...
int clockPin = 3;

void setup()
{
  ...  // Initialisation port serie à 115200 bauds
  Balance.begin(dataPin, clockPin);// Initialisation Hx711
} // Fin de setup

void loop()
{
... {  // Si un caractère est disponible sur le port série .available()
     ...;  // lire le caractère c disponible avec .read()
     ...;   //  Si c!=71 retour (Code ascii de G = 71)
     ...; // afficher Balance.read_average(10)
    while (Serial.available()) Serial.read(); // Vider le buffer série
} // Fin de Si un caractère est disponible
} // Fin de loop

Appel 2 : Présenter votre montage et votre programme au professeur.

Étape 3 : Exploitation et calculs (PV d’étalonnage)

Objectif : étalonner et estimer l'incertitude de notre balance

Téléchargez ce programme Labview.

Enregistrez-le dans le même dossier que votre programme Arduino Hx711_Base.ino

Sélectionner le port com de l'Arduino :

Ouvrir le fichier PV d’étalonnage Excel (formules supprimées).
Renseigner toutes les cellules à partir des résultats expérimentaux.

A l'aide de masses controlées par une balance de précision (0,1g)
    réaliser 7 à 10 points étalons régulièrement espacés sur la pleine echelle.
    Protocole conseillé :
    - Avant chaque point refaire le
    - Attendre 5 s aprés avoir posé la masse étalon avant de

Pour ce capteur c'est la valeur du zéro qui est le moins stable (sensible à la température notamment)
Aussi, pour limiter l'erreur d'offset, le protocole recommande de refaire le zéro avant chaque point.

Reporter les mesures : masse étalon m, valeur numérique N, dans TP_09_Balance_Excel

Calculer les écarts en g et en LSB par rapport au modèle constructeur déduit de la sensibilité théorique calculée à l'étape 1
La balance est-elle conforme à la demande client (EMT = 0,5 g) ?
La balance est-elle conforme à la doc constructeur du capteur de force ? (cf question 4 étape 1)

Appel 3 : Présenter votre étalonnage au professeur.

Etape 4 : Évaluer la fidélité et l’incertitude globale du système

Tracer la droite d’étalonnage et déterminer le modèle : $m = b_{1} \times N + b_{0}$
Correction : vérifier que le modèle corrigé est conforme à la demande client
Pour chaque point d’étalonnage, le résultat est jugé conforme si : $Résidu < EMT - U_{é talon}$
Pour U_étalon rechercher l'incertitude élargie d'une masse de 1kg de classe M1.
Rédigez une conlusion sur la justesse de la balance avant correction et après correction (au moins 5 lignes)

Récapitulatif des formules utilisées :

Correction m = __________________

résidus en g = ___________________________

résidus en LSB =_________________________

Conformité = SI(_______________________________________)
Calculer :
- le coefficient de détermination $R ²$ ,
- l’erreur-type $S_{ey}$ ,
- l’incertitude du modèle $U_{mod le} = t_{95%} \times S_{ey}$
Calculer l’écart-type expérimental s (fidélité) puis l’incertitude élargie associée : $U fidéli_{té} = k \times s$
Faire une conslusion sur la fidélité de la balance
Compléter le bilan d’incertitudes (k=2) :
- Masse étalon (type B) classe M1,
- Résolution (type B),
- Fidélité (type A),
- Modélisation (type A).
- → Calculer pour chacune : u, u² et la contribution relative %.
  Identifier les trois sources principales d’incertitude.
  $_{Faire une conlusion sur l'exactitude de la balance corrigée}$
Vérifier la conformité globale en s’assurant que :
$U_{totale} < EMT = 0, 5 g$
Pour chaque point d’étalonnage, le résultat est jugé conforme si : $Résidu < EMT - U_{é talon}$

Cette approche permet de couvrir le risque de déclarer une balance conforme alors qu’elle ne l’est pas.
Si toutes les conditions sont vérifiées, la balance est considérée conforme.

Analyse critique : à l'aide des documents ci-dessous justifiez pourquoi un professionnel de la métrologie tel que Deltamu ne se contente pas de cette méthode.
Noter les numéros des arguments qui sont pour (la méthode Excel) et ceux qui sont contre. Puis conclure.

Quelques mots de théorie

Il existe dans la littérature de nombreuses stratégies pour trouver un modèle à partir de données expérimentales. La plus classique, utilisée par Excel, repose sur une stratégie dite des « moindres carrés ». Apparemment simple, l’approche par les moindres carrés recouvre différentes possibilités plus ou moins élaborées

– Moindres carrés ordinaires (O.L.S.) qui ne traite que des valeurs de x (étalon) et de y (mesure) observées, sans tenir compte des incertitudes associées. Pour être utilisable, cette technique demande que quelques conditions soient respectées :

(1) Pas d’incertitude en x (ce qui n’est jamais le cas lors d’un étalonnage, mais on peut parfois la supposer négligeable),
(2) Incertitude identique sur les y (ce qui est rarement le cas en étalonnage car il est fréquent que l’incertitude soit proportionnelle à la valeur de x – cas des incertitudes qui s’expriment en %),
(3) Pas de covariance entre les incertitudes en y (ce qui est rarement le cas lors des étalonnages, pour les raisons évoquées ci-avant.

... (4) Si la correction n’est pas significative, l’écart-type des résidus s²_y/x sera une estimation acceptable de la performance (l’incertitude) du moyen de mesure dans un bilan de causes d’incertitude.

... (5) Par ailleurs, les techniques des moindres carrés permettent de calculer le modèle qui donne y (mesure) à partir de x (étalon).
Or, en métrologie, c’est le modèle inverse qui est utile, celui qui donne x (valeur « vraie ») en fonction de y (valeur physiquement mesurée).
Cette inversion du modèle impose une précaution essentielle car il ne suffit pas « d’inverser les colonnes » pour que ça fonctionne (même si les mathématiques – Excel – donnent toujours des valeurs…) !

... Cet article a pour objectif de sensibiliser à la problématique de la modélisation, qui ne peut pas se résumer à l’ajout d’une courbe de tendance via Excel.
Le monde de la métrologie est le monde des incertitudes, et tous nos calculs en sont entachés.

Pour pouvoir réutiliser votre étalonnage lors d'une prochaine séance (avec la même balance) :

En appuyant sur vous avez sauvé votre étalonnage dans le dossier du programme au format csv
CSV : Comma Separated Values, format texte de valeurs séparées par des "," ou ";".

Il suffira la séance suivante de cliquer sur pour sélectionner le fichier d'étalonnage que vous souhaitez utiliser.

Appel 4 : faites constater votre étalonnage et son incertitude au professeur
Un bonus sera accordé au groupe ayant la meilleure incertitude.

Le mode balance

Avant d'activer le mode balance, refaire le

L'approche des 5 M nous permet d'identifier de nombreuses sources d'erreurs dans une chaine de mesure.

Mesurande (Matières) : participe à l'incertitude du modèle.
Le corps d'épreuve est en aluminium, il peut se dilater, se déformer...
Milieu : la température et l'humidité varient peu durant la séance de TP.
par contre ce paramètre apportera de l'incertitude si on réutilise notre étalonnage dans plusieurs mois
Méthodes : le protocole du TP a pour but de minimiser les sources d'erreur :
                      Refaire avant chaque mesure le
                      positionner la charge toujours au milieu de la balance
                      attendre 5 s avant de lancer une mesure afin de laisser passer le transitoire
                      agir lentement pour éviter des vibrations....
Matériel : l'incertitude de la balance étalon doit-être prise en compte
le matériel utilisé est numéroté afin de réutiliser le même entre 2 séances.
Main d'œuvre : durant le TP un seul opérateur a manipulé pour minimiser cette erreur.

Etape 5 : Réaliser une Balance 100% Arduino (sans PC)

21. A l'aide de notre étalonnage réaliser un programme Arduino qui affiche la masse sur un écran LCD.

Balance.tare()
Prévoir dans le setup l'appel de la méthode .tare()
Cette méthode revient à :
zero= balance.read_average(10);
Balance.set_scale(s)
Utiliser aussi dans le setup la méthode .set_scale(s)
s étant la sensibilité en LSB/g déterminée lors de l'étalonnage
Plus rapide, la sensibilité peut se calculer sur un seul point :
sensibilite = (Nbrut - zero) / masse;
Balance.get_units(10)
Lire grâce à la méthode .get_units(10) la masse directement en grammes
correspondant à la moyenne de 10 mesures.
Cette méthode revient à :
Nbrut= balance.read_average(10);
masse= (Nbrut - zero) / sensibilite;
Prévoir un bouton poussoir pour appeler la méthode .tare()
Autre possibilité : Balance.read_average(10)
Au lieu d'utiliser les méthodes ci-dessus, on peut n'utiliser que la méthode .read_average(10) :

1. dans le setup on mesure : zero= balance.read_average(10);
2. dans le loop on mesure : Nbrut= balance.read_average(10);
3. puis on calcule : masse= (Nbrut - zero) / sensibilite;

Avantage : on peut ici garder la compatibilité avec notre programme communicant avec Labview sans réduire sa vitesse.

Appel 5 : Présenter votre programme balance LCD au professeur.

22. Amélioration : pour corriger la dérive du gain,
pour changer de balance rapidement,
proposer dans le setup un calibrage :

       - BP to tare (diapo 1) :
         Valider chaque étape par l'appui sur le Bouton Poussoir S1 (diapo 2)
         BP appuyé : digitalRead(BP) = False
         while (digitalRead(BP)); // Boucle d'attente tant que l'on a pas appuyé sur BP
         faire une tare sur 10 pts zero= balance.read_average(10);

      - BP to scale (diapo 3) :
        demander à l'utilisateur de placer une masse connue (par exemple 1 kg)
        attendre l'appui de BP (diapo 4), puis
        Nbrut= balance.read_average(10);
        calculer la sensibilité s à partir de ce point de mesure
       sensibilite = (Nbrut - zero) / masse;
        afficher sur la première ligne de l'écran la sensibilité (diapo 5),
        et sur la deuxième ligne la masse mesurée.

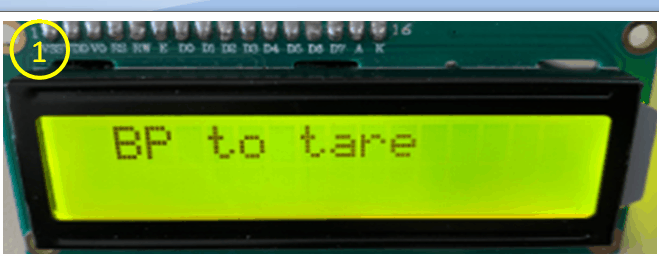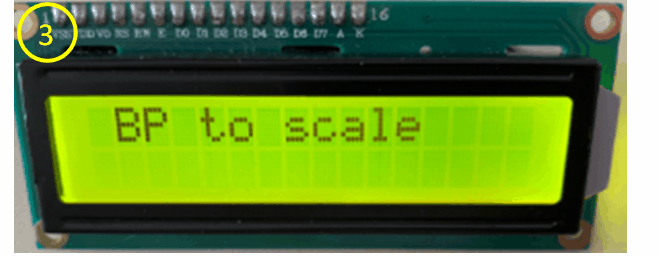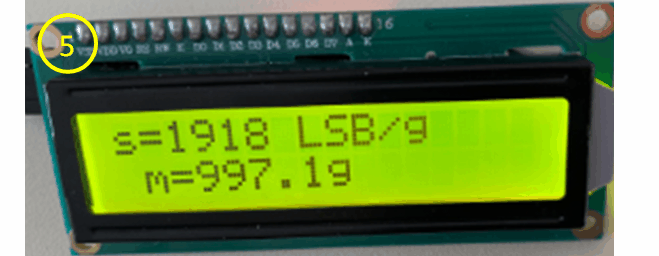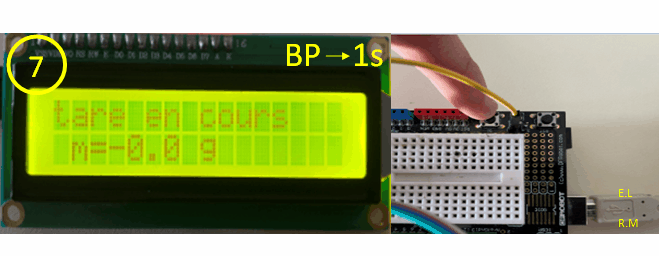Puis en mode mesure (loop) le BP S1 déclenche la tare (diapo 6) :

- Si BP est appuyé appeler le sous programme BP2tare()
attention, il faut appuyer sur BP durant 1s environ (diapo 7).

      -   void BP2tare() {
         afficher "tare en cours" durant cette opération
         zero= balance.read_average(10);}
        afficher de nouveau la sensibilité une fois la tare finie.

Conseil : inspirez vous du programme

Quels sont les avantages et inconvénients de cette méthode par rapport à un étalonnage ?

Appel 6 : Présenter votre programme balance LCD amélioré au professeur.