Tracer
et analyser des courbes :
Les tableaux : manipulation de base sur les tableaux
Les clusters : le cluster de points
Tracer un graphe :
Les nœuds de propriétés : manipuler les curseurs
Évaluation :
7 Tracé de courbes de
Lissajous
8 u(t) = U sin (2πf t + φ)
9 diagramme de Bode et analyse
Amélioration : le balayage logarithmique
Les
tableaux :
C’est une structure de données qui permet de « manipuler »
simultanément plusieurs données élémentaires du même type.
Par exemple un tableau de valeurs de mesures de nombres réels
On le caractérise par le type de la variable et une variable n donnant le nombre d’éléments. (numérotés de 0 à n-1).
Les
étapes pour créer un tableau DBL
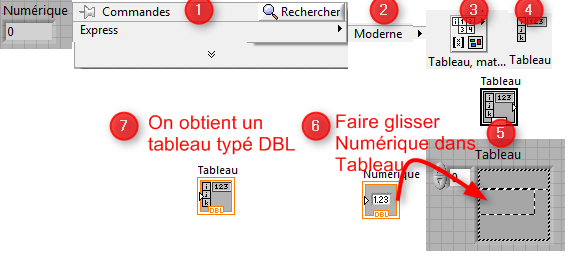
1 à 4 : Palette Commandes
/Moderne/Tableau,
mat.../Tableau
5 : On obtient un tableau vierge : sans type de variable
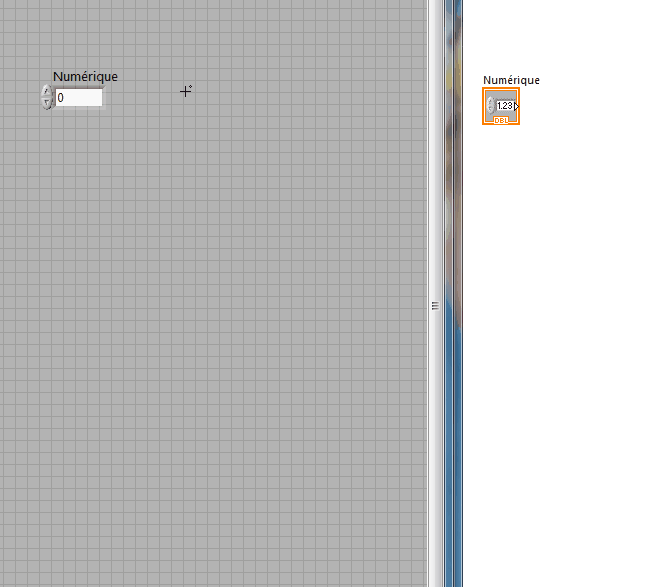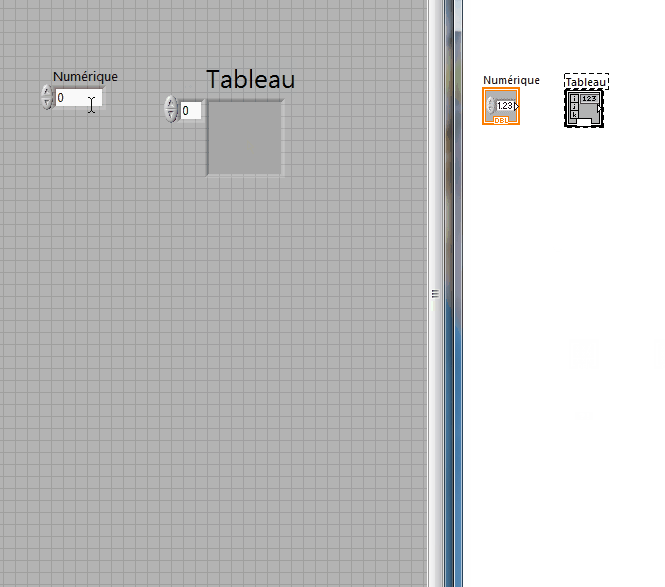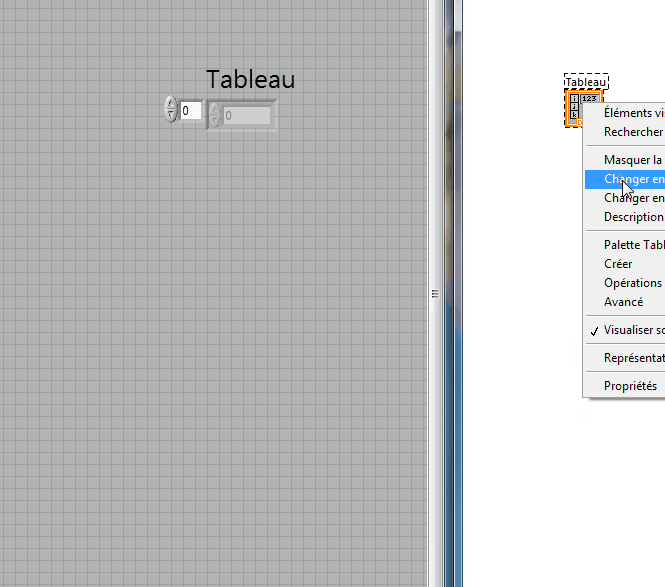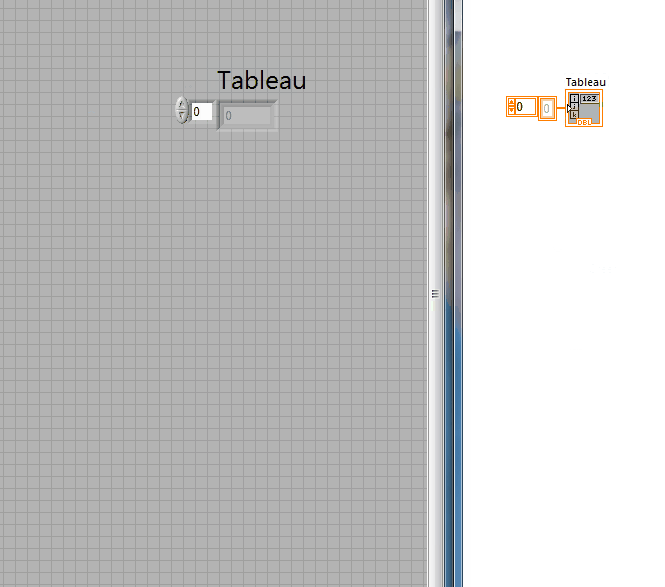
6 : On fait glisser dans le tableau une variable du type souhaité
:
ou
ou
ou 
...
7 : On obtient un tableau du type souhaité
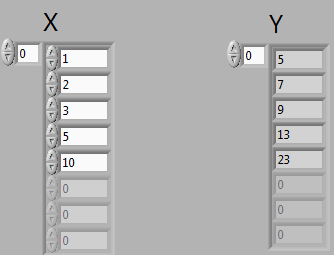Exercice
d'application 1 :
Créer un tableau de commandes X en DBL.
Créer un tableau Y d'indicateurs en DBL.
avec Y = 2*X+3
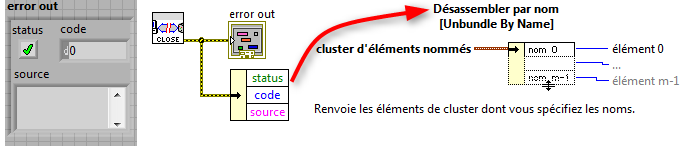Les clusters :
Les clusters regroupent des éléments de données de types différents.
Le cluster d'erreur LabVIEW est un exemple de cluster ; il comprend une valeur booléenne, une valeur numérique et une chaîne.
Les clusters sont semblables aux enregistrements ou aux structures des langages de programmation textuels.
Nous pouvons aussi faire un tableau de cluster.
Les coordonnées d'un point : le cluster de point
Pour mémoriser un point d'une courbe, nous allons assembler
ses coordonnées X et Y pour former un cluster représentant ce point.
Les coordonnées de la courbe seront l'ensemble des clusters de points mis dans un tableau.
Cette façon de procéder nous permettra par la suite d'utiliser
des fonctions évoluées de LabVIEW telle que :
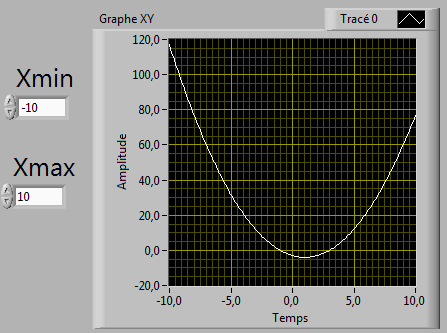Exercice
d'application 2 :
But : assembler dans un tableau les clusters des coordonnées d'une courbe.
Face avant : 2 commandes numériques Xmin et Xmax
Pas de calcul : Xn+1 = Xn + 0.1
Fonction à représenter : Y = x**2 - 2*x -
3
ou n'importe qu'elle fonction de votre choix.
Représenter cette fonction grâce à un graphe XY
Tracé d’un graphe :
Les types de graphes utilisés pour le tracé d’un signal sous LabVIEW sont :
Graphe
déroulant : l’échelle varie au cours du temps et la courbe est
tracée en direct mesure par mesure.
Graphe
: la courbe est tracée lorsque tout les points sont disponibles. En
X le numéro de mesure, en Y la mesure sous forme de tableau.
Graphe
XY : la courbe est tracée lorsque tout les points sont
disponibles. Il faut pour chaque point fournir les coordonnées X et
Y sous forme de tableau.
Graphes
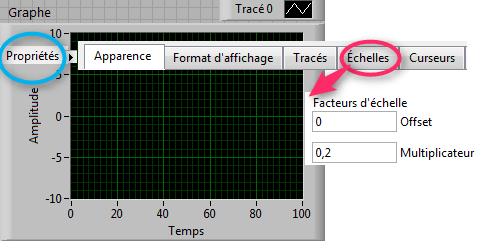
Ce type de graphique est utilisé lorsque l’unité de l’axe des X est l’indice du tableau de mesures.
Si une mesure est réalisée toutes les 0,2s,
il suffit de mettre comme coefficient multiplicateur 0,2 dans Propriété → onglet Echelles → Facteur d'échelle Multiplicateur
Remarque : sur un graphe nous pouvons ajouter des curseurs, alors que sur un graphe déroulant nous ne disposons pas de cette option...
Exercice d'application 3 : Graphe déroulant, entrée nombre
Contrôler toutes les 0,2s la valeur d'une commande numérique et l'afficher sur un graphe déroulant.
Vérifier que l'échelle des temps est cohérente.
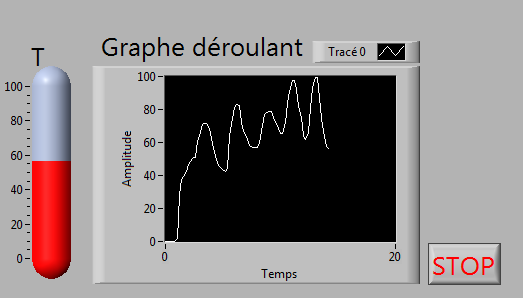
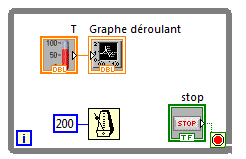Pensez
au facteur d'échelle pour le graphe...
Exercice
d'application 4 : Graphe, entrée tableau
Réaliser un graphe commandé par un tableau.
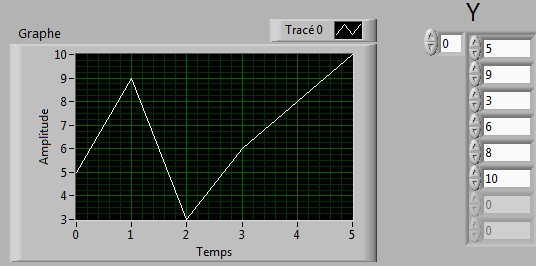
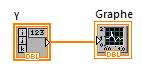
Le graphe XY
Ce type de graphique est utilisé lorsque l’unité de l’axe des X est un tableau de même taille que celui des mesures Y.
Pour tracer la courbe, il suffit de connecter sur le graphique les 2 tableaux de mesures X et Y assemblés.
3 possibilités :
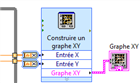soit
on utilise le VI Express Construire un graphe XY généré
automatiquement avec le graphe XY
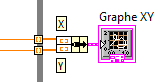
soit on le remplace par un cluster qui assemble le tableau des X
et le tableau des Y
c'est assez proche de ce que réalise le VI Express Construire un
graphe XY
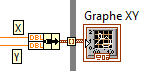soit
on assemble les coordonnées X,Y dans un cluster de point
et on réunit les points dans un tableau de cluster.
Cette solution permet d'accéder par la suite à des fonctions
évoluées de la palette Tableau.
Algorithme pour construire une courbe XY
Plutôt que de remplir un tableau X manuellement, on peut le calculer, à l’aide d’une boucle For, en connaissant Xmin, Xmax et le nombre N de points à calculer.
Avec ceci on calcule le Pas de calcul entre 2 mesures :
Exemple : y = x3- 2x2 - 3x avec Xmin = 0 ; Xmax = 5 pour N = 1000 points calculés
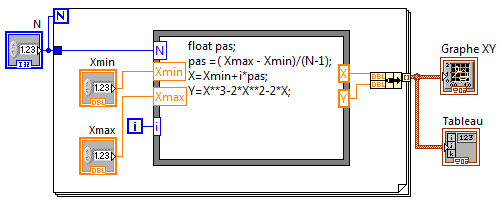
Par la suite on remplacera le calcul par des mesures. L'algorithme restera le même pour le calcul du pas.
Exemple : relevé automatique du diagramme de Bode pour
un filtre
L'utilisateur donne fmin, fmax et N le nombre
de point à mesurer.
f remplace alors X, on calcule le pas et on envoie au GBF la
fréquence f souhaitée.
Puis on mesure la tension de sortie qui joue le rôle de Y.
Exercice
d'application 5 : Graphe XY, entrée un tableau de cluster de points.
Tracer y = x3- 2x2 - 3x avec Xmin = -2 ; Xmax = 3 pour N = 1000 points calculés.
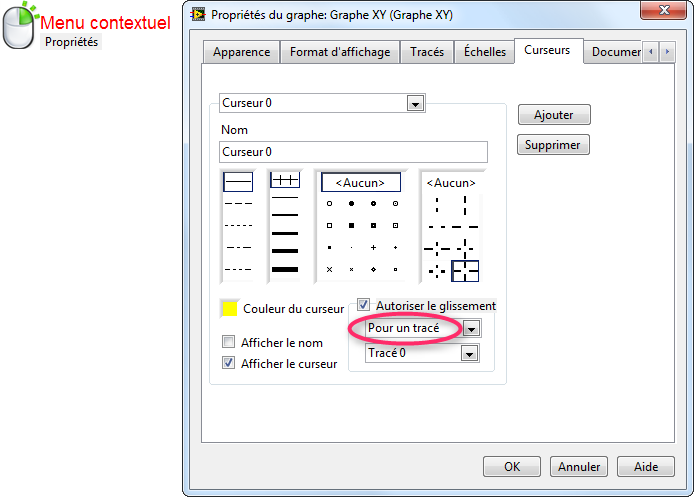
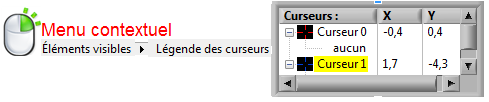
Ajouter 2 curseurs à la courbe. Afficher la
légende des curseurs.
Déterminer à l'aide des curseurs les coordonnées des 2 points où la
dérivée de cette courbe est nulle.
Les
nœuds de propriétés :
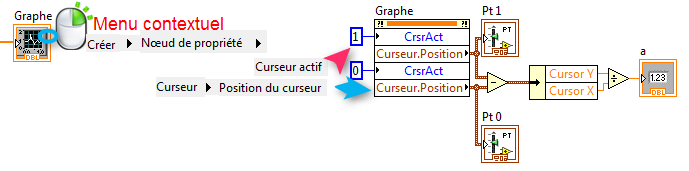
On peut aussi programmer de façon dynamique les propriétés d'un objet grâce au nœud de propriété.
Le nœud de propriété vous permet d'accéder à toutes les
propriétés d'un objet.
Elles sont nombreuses , par conséquent les menus proposés sont
denses.
Vous pouvez aussi bien lire (Lecture) qu'écrire (écriture) des propriétés.
Par exemple vous pouvez sélectionner un curseur (
)
puis lire sa position (
).
Exercice
d'application 6 : les nœuds de propriétés
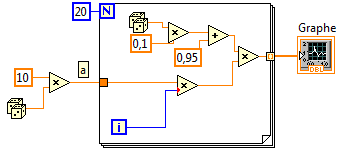
1. Réaliser le diagramme suivant.
Écrivez l’équation réalisée par ce diagramme.
2. Ajoutez 2 curseurs à la courbe. Afficher la légende des curseurs.
3. A l'aide d'un nœud de propriété, récupérer
les coordonnées des points des curseurs.
Calculer à l'aide de ces points le coefficient directeur de
la droite passant par ces 2 points.
4. Calculer a (coefficient directeur de la
droite)
à l’aide du VI express (situé dans « Analyse ») « Ajustement
de courbes ».
Exercice
7 : Tracé de courbes de Lissajous
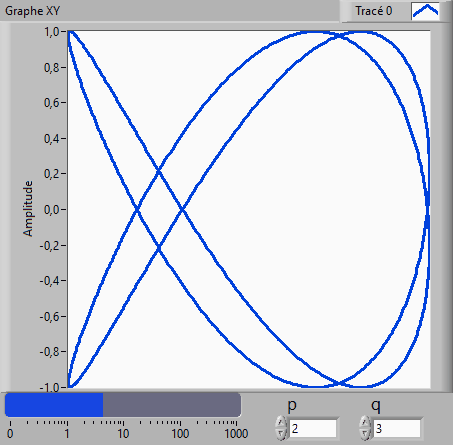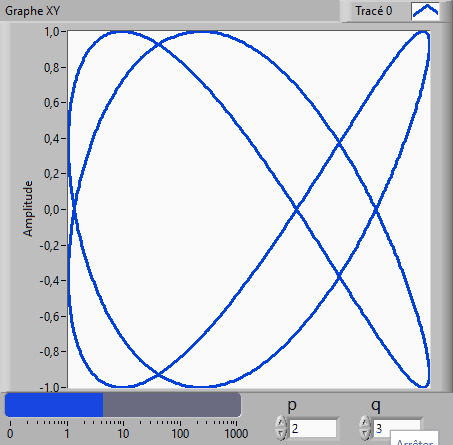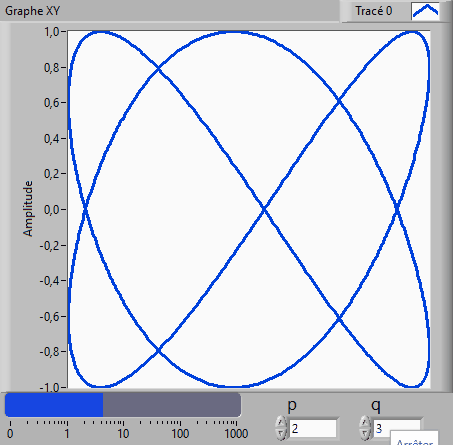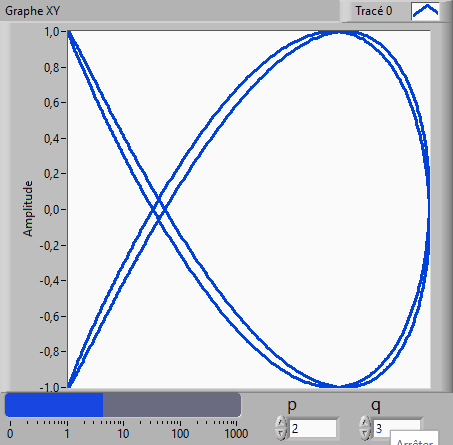
Une courbe de Lissajous peut être définie par l'équation paramétrique suivante :
x(θ) = a*sin(p*θ)
y(θ) = b*sin(q*θ + φ)
On prend a = b = 1.
Conseils : utiliser un graphe XY et une boite de calcul ...Labview for dummies
1. Réaliser un diagramme permettant de tracer
une courbe de Lissajous.
p, q et phi seront modifiables sur la face avant.
2. Faire varier le paramètre θ de 0 à 2π et calculer 1000 points de mesures.
3. Faites des essais avec p=2, q=3 et
phi=0 ; p=3, q=4 et phi=0.
Enfin pour p =1, q=1 et φ = 90° puis φ =
45 ° puis φ = 0°.
4. Animer la courbe de Lissajous en incrémentant φ de 0,1° à chaque itération.
Sur un oscilloscope on obtient la courbe de
Lissajous en mode XY.
Lorsque les 2 voies sont à la même fréquence on obtient une ellipse
qui nous
permet de calculer φ.
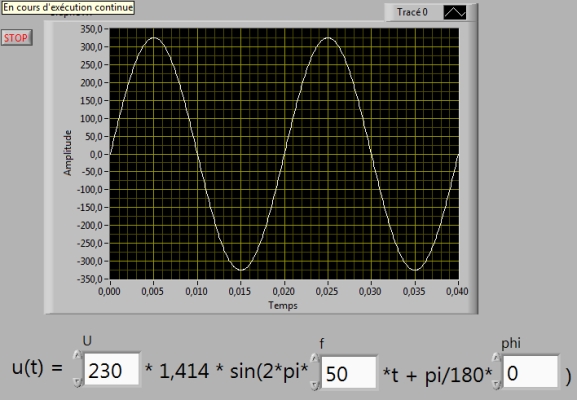
Exercice 8 : Graphe XY échelle linéaire
Écrire le programme permettant d’afficher sur un
graphe la fonction :
u(t) = U sin (2πf t + φ) pour t compris entre 0 et Tmax.
Le nombre de points N, l’amplitude U, f, phi en degré et Tmax seront modifiables sur la face avant.
Le graphe doit être gradué en temps. L’échelle temporelle est linéaire.
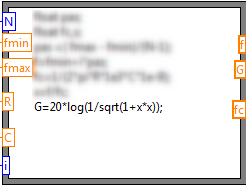Exercice 9 : Graphe XY échelle logarithmique
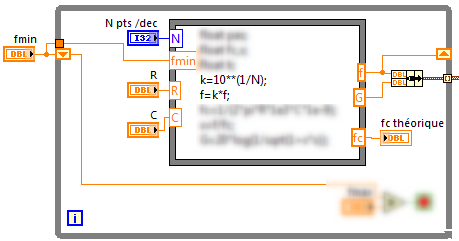
1. Écrire un programme permettant d’afficher sur un graphe la courbe de réponse en fréquence d’un filtre RC passe bas, rappel des équations :
R,C, fmin, fmax et N (nb de points calculés) sont modifiables grâce à une commande numérique.
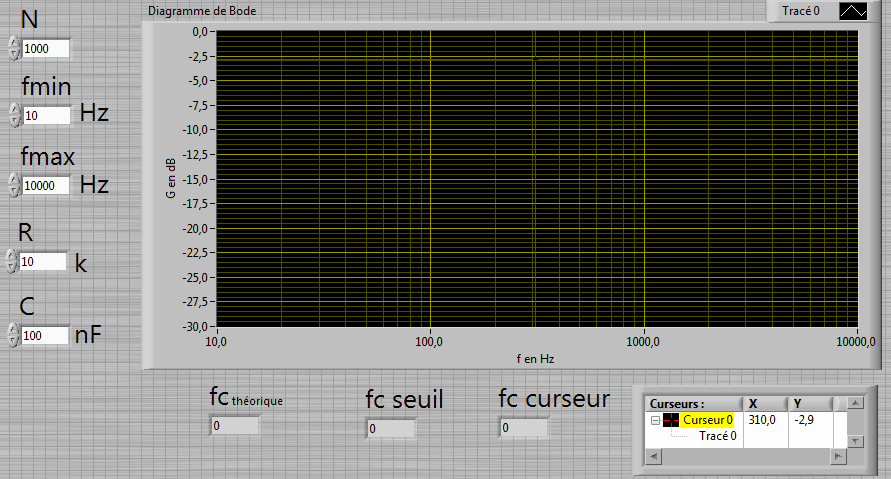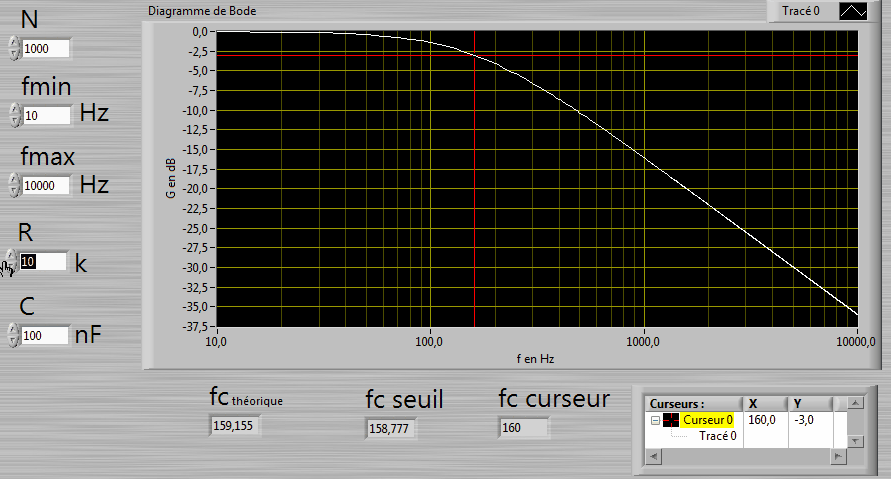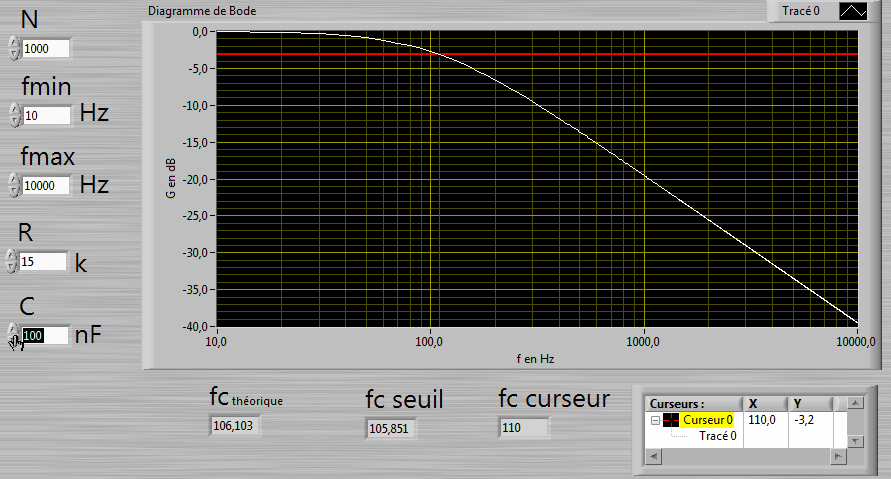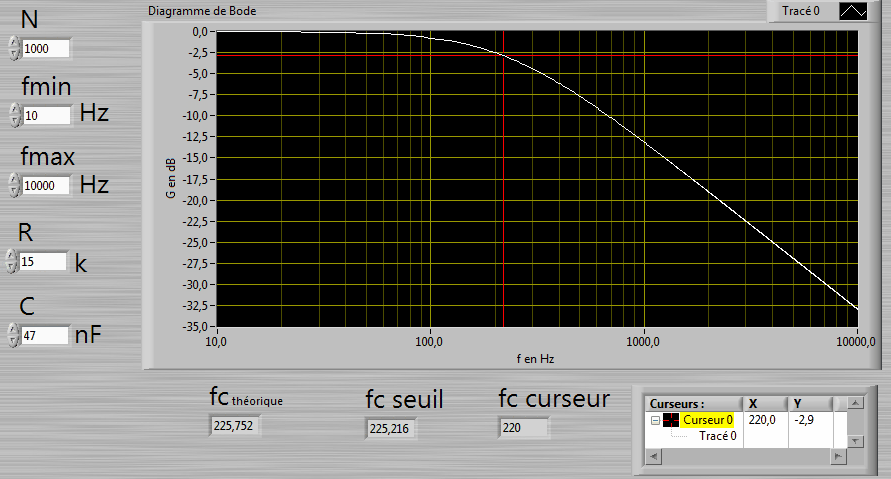
2. Calculer et afficher fc théorique.
3. Le graphe G(f) utilisera en abscisse une échelle logarithmique (1000 points régulièrement espacés entre fmin et fmax) qui sera graduée en Hz.
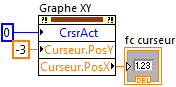4. Puis placer automatiquement un curseur sur la
courbe à G = -3dB.
Afficher la fréquence fc curseur.
Pour N = 30, la fréquence de coupure trouvée est-elle précise ?
5. Utiliser la fonction seuil d'un tableau pour
interpoler plus précisément la fréquence de coupure.
Afficher fc seuil.
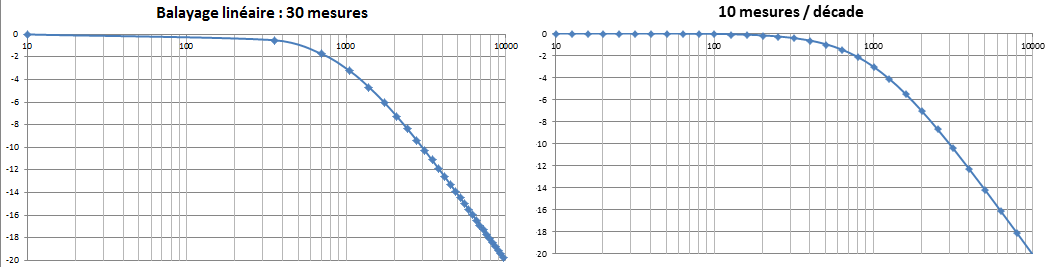
Amélioration : le balayage logarithmique
Comme
le montre l'étude ci-dessus un balayage linéaire sur une echelle
logarithmique n'est pas équilibré.
En musique :
La gamme tempérée est un système d'accord qui divise l'octave en douze intervalles chromatiques égaux.
Le rapport d'octave étant égal à 2 et contenant douze intervalles égaux (12 demi-tons) en progression géométrique, soit 2 = r12 => r = 21/12
On calcule la fréquence (note) suivante par la relation de récurrence : fn+1 = fn*21/12
En électronique :
Si je veux faire un balayage logarithmique avec N points par octave : fn+1 = fn*21/N
Si je veux faire un balayage logarithmique avec N points par décade : fn+1 = fn*101/N
Une décade est un facteur de 10 entre deux nombres.
C'est un concept important dans les représentations graphiques de
type logarithmiques, en particulier pour les fréquences
Le facteur de 10 d'une décade peut s'interpréter dans les deux
directions : la décade supérieure de 100 Hz (102) est
1 000 Hz (103) , et la décade inférieure est 10 Hz
(101) .
Remarques sur
LabVIEW :
- une relation de récurrence s’écrit facilement avec un registre à décalage…
- Condition d’arrêt pour une boucle While : f > fmax
Un peu de math :
Il s’agit d’une suite géométrique
de raison r :
On souhaite avoir au rang n une
fréquence 10 fois plus élevée :
Nous en déduisons l’expression de r :
Autre écriture possible au rang i : fi = fmin ri = fmin*10i/N
Utile si on ne veut pas utiliser de registre à décalage...
6. Améliorer le programme en effectuant un balayage logarithmique.
Pour N = 10 pts/décade relever Fc trouvée par le curseur.
Comparer cette valeur à celle trouvée pour un balayage
linéaire avec N = 30