Modéliser une CTN
Comment modéliser une CTN ?
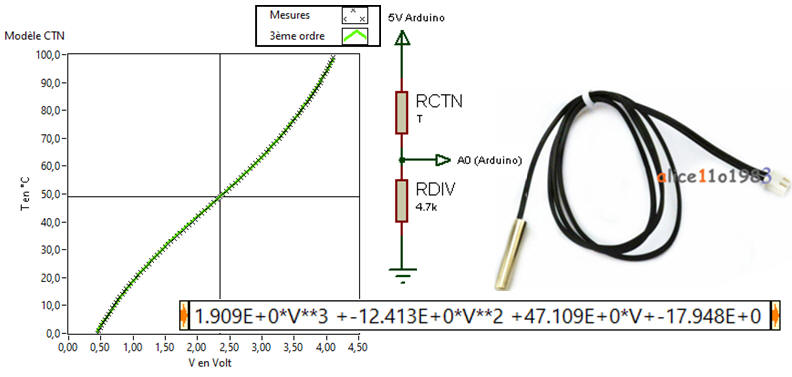
Une CTN est une thermistance à faible coût qui ne nécessite qu'un pont diviseur pour être mise en oeuvre.
Par contre une bonne modélisation de ce montage n'est pas une droite mais un polynôme d'ordre 3.
Trouver ce polynôme à partir des caractéristiques constructeur de la CTN ( R25 et β) et de la résistance du pont diviseur est complexe.
Aussi nous allons réaliser une application Labview qui réalise
cette tâche automatiquement
et la garder précieusement pour mettre en œuvre rapidement une CTN.
Cahier des charges :
- Créer ces entrées sur la face avant:
→ R25 = 10 kΩ β = 3950 K (valeurs par défaut : celles des CTN de la J101)
→ Rdiv = renseignée par l'utilisateur après conseil du programme
→ Gamme : de Tmin à Tmax
Calculer sur 100 points la tension de sortie en V du montage en fonction de la Température T en °C
Tracer T(V) sous forme de points - Modéliser T(V) par un polynôme d'ordre 3.
Tracer ce polynôme sur le même graphe que T(V)
Afficher ce polynôme sous forme d'une chaîne de caractères
afin que l'utilisateur puisse la copier et la coller dans un noeud d'expression de son programme
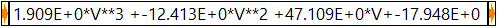
- Calculer les résidus entre le modèle et les points calculés,
calculer l'écart type des résidus Sn-2
en déduire umodele l'incertitude type de prédiction du modèle.
Afficher Umodèle en °C. - Ajouter un curseur sur le graphe sur le tracé du modèle,
afficher pour ce curseur la température, la tension et la sensibilité du montage pour ce point.
Calculer les incertitudes à la position du curseur. - Mettre en oeuvre une CTN avec un multimètre.
Etape 1 : Tracé de T(V)
Les thermistances, comme les capteurs de température à résistance
(RTD), sont des semi-conducteurs thermosensibles dont la résistance
varie avec la température.
Les thermistances sont constituées d’un matériau semi-conducteur
d’oxyde métallique encapsulé dans une petite bille d’époxy ou de
verre.
En outre, les thermistances présentent généralement des valeurs de
résistance nominale plus élevées que les RTD (de 2 000 à 10 000 Ω)
et peuvent être utilisées pour de plus faibles courants...
Les thermistances ont une sensibilité de mesure très élevée, ce qui
les rend très sensibles aux variations de températures.
Les thermistances coûtent beaucoup
moins cher qu'une PT100 (RTD), et il suffit d'un simple diviseur de
tension pour les mettre en oeuvre.
Elles sont très utilisées dans l'industrie.
La thermistance étudiée possède un Coefficient de Température Négatif (CTN), c’est à dire que la résistance diminue quand la température augmente.
La loi de variation de la résistance d’une CTN en fonction de la
température est donnée par la formule :
-
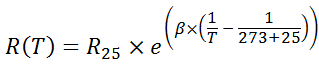
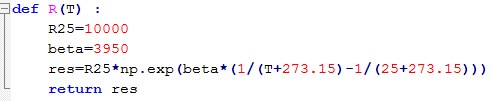avec : R25 valeur de la résistance à T = 273+25 =
298 K (attention dans cette formule il faut exprimer T en K ! ) -
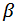: indice de sensibilité
thermique en K (beta) - R(T) est la résistance (en ohms) du capteur à la température T cherchée (en Kelvins);
Nous disposons de cette CTN en J101 :
- Measurement range: -20 to 105 °C
- Length of wire: 1 meter
- Type: NTC 10 kΩ ±1% 3950
Rappel : lors du TP
régulation Arduino nous avons utilisé un
tableau Excel
pour faire les calculs. (Plus des
macros pour
changer d'ordre)
Nous allons aujourd'hui réaliser les mêmes fonctions dans un
vi plus convivial à utiliser.
1.
Prévoir une face avant ayant les entrées et indicateurs suivants :
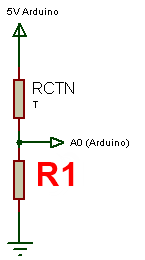
Le conditionneur est un simple pont diviseur.
On démontre que l'on optimise la sensibilité du pont lorsque R1 est
proche de la résistance de la CTN au milieu de la gamme.
2. Dans une boite de calcul, calculer (R, T et V en gras = tableau)
→ Tmilieu : la
température du milieu de la gamme
→ R1milieu : la résistance correspondant au milieu de
gamme
→ dt : le pas en °C entre 2 calculs (comme dx)
→ T
: les 100 températures choisies de manière uniforme dans la gamme
→ R : les résistances de la CTN
correspondantes
→ V : la tension aux bornes de R1
calculée à l'aide d'un diviseur de tension
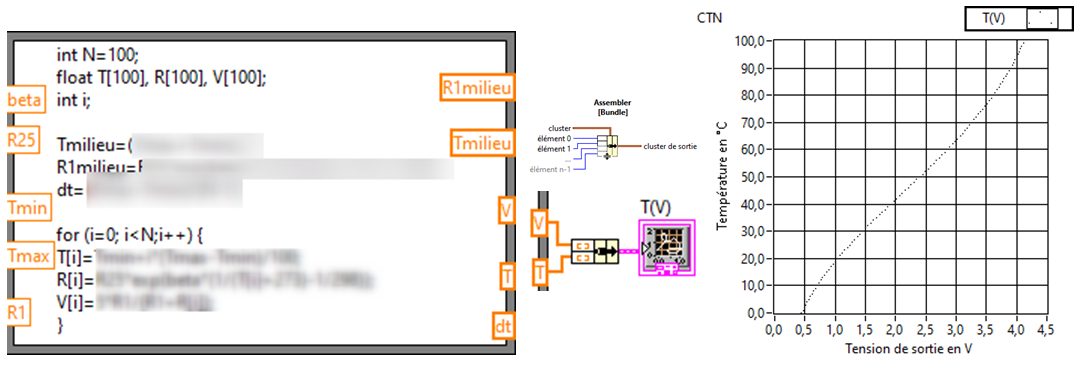
3. Tracer T(V)
Etape 2 : Modéliser T(V) par un polynôme d'ordre 3
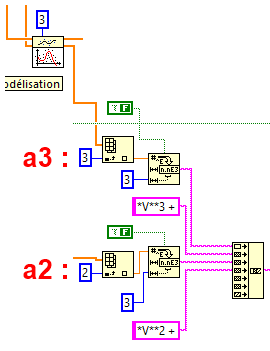
4. Modéliser T(V) par un polynôme d'ordre 3.
Un ordre 2 ne suffit pas car
il y a un
point d'inflexion.
Tracer ce polynôme sur le graphe précédent.
5.
Récupérer les coefficients du polynôme et les afficher sous forme d'une chaîne de caractères
afin que l'utilisateur puisse la copier et la coller dans un
noeud d'expression de son programme.
Les coefficients sont donnés sous
forme de tableau :
T = a3*V3 + a2*V2
+ a1*V1 + a0*V0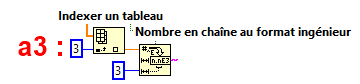
L'utilisateur peut ensuite copier et coller la
chaîne dans un
noeud d'expression de son programme
Appel 1 : Faîtes constater le bon fonctionnement de votre programme au professeur.
Etape 3 : Evaluation de l'erreur de prédiction
Le modèle obtenu n'est pas parfait, on souhaite estimer l'erreur de prédiction dûe à l'utilisation de ce modèle.
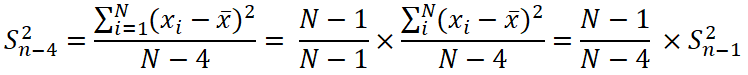5. Calculer les résidus entre les températures
calculées (mesurande) et les températures du modèle (prédiction).
Résidus = Tmodèle-T
Calculer l'erreur type de prédiction du modèle :
Sey = Sn-4
= écart-type des résidus pour un ordre 3 (n-4 degrés de libertés)
Appliquer le facteur d'élargissement k, pour déterminer
l'incertitude élargie (95%) du modèle : Umodèle
Il y a toujours un polynôme d'ordre :
→
1 (T=a1*V+a0)
qui passe par 2 pts (c'est une droite) => n-2
degrés de liberté =>
Sey = Sn-2
= écart-type des résidus pour un ordre
1
→ 2
(T=a2*V2+a1*V+a0) qui
passe par 3 pts => n-3 degrés de
liberté =>
Sey = Sn-3
= écart-type des résidus pour un ordre
2
→ 3
(T=a3*V3+a2*V2+a1*V+a0)
qui passe par 4 pts => n-4 degrés
de liberté =>
Sey = Sn-4
= écart-type des résidus pour un ordre
3
Pour un échantillion de 101 variables aléatoires
on peut confondre Sn-1 et Sn-4= 1,015*Sn-1
6. Pour mesurer une température intérieure,
quelle gamme et R1 choisir ?
Quelle incertitude élargie (95%) est alors apportée par le
modèle ?
Appel 2 : Faîtes constater le bon fonctionnement de votre programme au professeur.
Etape 4 : Sensibilité du montage
Contrairement à un capteur linéaire, la sensibilité de notre CTN est variable.
Si nous mesurons la tension avec un Arduino ayant une "précision"
(incertitude élargie à 95%) de ±10 mV,
nous avons besoin de connaître la sensibilité du montage pour
transformer cette "précision" en °C.
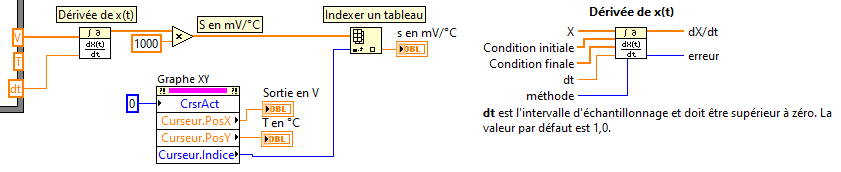
7. Pour chaque point, calculer la sensibilité du
montage s=dV/dT
Exprimer cette sensibilité en mV/°C
8. Ajouter un curseur à la courbe.
Pour la position du curseur indiquer la sensibilité du
montage en mV/°C
9.
Déterminer la sensibilité maximale et la sensibilité minimale du
montage.
attention la première et la dernière sensibilités ne sont
pas à prendre en compte
le calcul de la dérivée nécessite la valeur d'avant et
d'après...
Pourquoi l'industrie préfère des PT100 plus chères à mettre en
oeuvre que des CTN ?
10. Pour une gamme 0 - 50°C R1 = 10 kΩ
déduire :
- l'erreur dûe à l'Arduino en °C
- l'erreur maximale que fait l'Arduino sur la
gamme.
Pour cette gamme remplir ce tableau récapitulatif :
| T en °C | 5 | 25 | 45 | Gamme complète |
| Uctn | ||||
| Uarduino | ||||
| Umodèle | ||||
| Utotal |
Rappel : Uctn = 0.01*abs(t-25) + 0.25 ; // 1% de la mesure ± 0,25°C avec une référence à 25°C
11. Modifier votre programme pour que tous ces
calculs d'incertitudes se fassent automatiquement,
T est déterminé par la position du curseur.
Umodèle pour cette gamme est-il trop important ?
12. Reprendre le tableau pour la gamme complète du capteur de -20°C à 105°C R1=4,7 kΩ :
| T en °C | -7.5 | 42.5 | 92.5 | Gamme complète |
| Uctn | ||||
| Uarduino | ||||
| Umodèle | ||||
| Utotal |
Conclure sur l'importance de bien choisir la
gamme de modélisation de la CTN.
Si on avait laissé sur cette gamme une résistance R1= 10 kΩ,
que constatez-vous ?
13. Enregistrer votre programme CTN.vi : il vous sera utile pour chaque mise en oeuvre d'une CTN.
Appel 3 : Faîtes constater le bon fonctionnement de votre programme au professeur.
Etape 5 : Mise en oeuvre d'une CTN et de notre application
14. Déterminer le meilleur modèle pour mesurer une température intérieure avec notre CTN.
15. Réaliser un nouveau VI qui :
- Lit la mesure de la tension du montage d'un
multimètre FI2960MT
- Calcule la température associée
16.
Sur une gamme de 0 à 5 V, calculer UFI2960MT(en V)
En déduire l'incertitude maximale en °C dûe
au FI2960MT.
Vous semble-t-elle négligeable ?
17. Calculer automatiquement U l'incertitude de votre mesure.
Appel 4 : Faîtes constater le bon fonctionnement de votre programme au professeur.